Completing perfect complexes

Abstract

This note proposes a new method to complete a triangulated category, which is based on the notion of a Cauchy sequence. We apply this to categories of perfect complexes. It is shown that the bounded derived category of finitely presented modules over a right coherent ring is the completion of the category of perfect complexes. The result extends to non-affine noetherian schemes and gives rise to a direct construction of the singularity category. The parallel theory of completion for abelian categories is compatible with the completion of derived categories. There are three appendices. The first one by Tobias Barthel discusses the completion of perfect complexes for ring spectra. The second one by Tobias Barthel and Henning Krause refines for a separated noetherian scheme the description of the bounded derived category of coherent sheaves as a completion. The final appendix by Bernhard Keller introduces the concept of a morphic enhancement for triangulated categories and provides a foundation for completing a triangulated category.

1 Introduction

This note proposes a new method to complete a triangulated category, and we apply this to categories of perfect complexes [17]. For any category ${\mathcal {C}}$, we introduce its sequential completion ${\widehat{{\mathcal {C}}}}$, which is a categorical analogue of the construction of the real numbers from the rationals via equivalence classes of Cauchy sequences, following Cantor and Méray [5, 27].

When a ring $\Lambda$ is right coherent, then the category ${\text {mod }}\Lambda$ of finitely presented modules is abelian and one can consider its bounded derived category ${\mathbf {D}}^b({\text {mod }}\Lambda )$, which contains the category of perfect complexes ${\mathbf {D}}^\mathrm {per}(\Lambda )$ as a full triangulated subcategory. The following theorem describes ${\mathbf {D}}^b({\text {mod }}\Lambda )$ as a completion of ${\mathbf {D}}^\mathrm {per}(\Lambda )$.

Theorem 1.1

For a right coherent ring $\Lambda$ there is a canonical triangle equivalence

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}(\Lambda )}^b\xrightarrow {\ _\sim \ }{\mathbf {D}}^b({\text {mod }}\Lambda ) \end{aligned}$$

which sends a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}(\Lambda )$ to its colimit.

The description of ${\mathbf {D}}^b({\text {mod }}\Lambda )$ as a completion extends to non-affine schemes. Thus for a noetherian scheme ${\mathbb {X}}$ there is a canonical triangle equivalence

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}^b\xrightarrow {\ _\sim \ }{\mathbf {D}}^b({\text {coh }}{\mathbb {X}}). \end{aligned}$$

In particular, this provides a direct construction of the singularity category (in the sense of Buchweitz and Orlov [4, 37]) as the Verdier quotient

$$\begin{aligned} \frac{\widehat{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}^b}{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}. \end{aligned}$$

The completion ${\widehat{{\mathcal {C}}}}$ of a category ${\mathcal {C}}$ comes with an embedding ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ so that the objects in ${\widehat{{\mathcal {C}}}}$ are precisely the colimits of Cauchy sequences in ${\mathcal {C}}$, and ${\widehat{{\mathcal {C}}}}$ identifies with a full subcategory of the ind-completion of ${\mathcal {C}}$ in the sense of Grothendieck and Verdier [14].

When ${\mathcal {C}}$ is triangulated, there is a natural finiteness condition such that ${\widehat{{\mathcal {C}}}}$ inherits a triangulated structure with exact triangles given as colimits of Cauchy sequences of exact triangles in ${\mathcal {C}}$. This involves the notion of a phantom morphism and Milnor’s exact sequence [28]. In order to explain this, let us assume for simplicity that ${\mathcal {C}}$ identifies with the full subcategory of compact objects of a compactly generated triangulated category ${\mathcal {T}}$. Fix a class ${\mathcal {X}}$ of sequences $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {C}}$ that is stable under suspensions. We consider their homotopy colimits and have

$$\begin{aligned} {\text {Ph }}(\mathop {\mathrm{hocolim }}\limits _iX_i, \mathop {\mathrm{hocolim }}\limits _jY_j)=0\quad \text {for all}\quad X,Y\in {\mathcal {X}}\end{aligned}$$

if and only if

where ${\text {Ph }}(U,V)$ denotes the set of phantom morphisms $U\rightarrow V$. It is this finiteness condition which is satisfied for categories of perfect complexes, and it enables us to establish a triangulated structure for the completion of ${\mathcal {C}}$ with respect to ${\mathcal {X}}$.

The idea of completing a triangulated category ${\mathcal {C}}$ is not new; the method is always to identify the completion ${\mathcal {D}}$ with a category of certain cohomological functors ${\mathcal {C}}^\mathrm {op}\rightarrow \mathrm {Ab}$. Note that the category of all cohomological functors is equivalent to the ind-completion of ${\mathcal {C}}$. In most cases, ${\mathcal {C}}$ identifies with the category of compact objects of a compactly generated triangulated category ${\mathcal {T}}$, and ${\mathcal {D}}$ is another triangulated subcategory of ${\mathcal {T}}$. Let us mention the paper of Neeman [29] that addresses the question when a category of cohomological functors carries the structure of a triangulated category. In [38], Rouquier identifies various natural choices of cohomological functors ${\mathcal {C}}^\mathrm {op}\rightarrow \mathrm {Ab}$. The recent work of Neeman [34, 35] employs the notion of ‘approximability’; it is crucial for understanding the case of non-affine schemes and recommended as an alternative approach via Cauchy sequences.

We also include a discussion of completions for abelian categories. Again, some finiteness condition is needed so that the completion is abelian. For instance, we show for a noetherian algebra $\Lambda$ over a complete local ring that the completion of the category ${\text {fl }}\Lambda$ of finite length modules identifies with the category of artinian $\Lambda$-modules. Using Matlis duality, this yields for $\Gamma =\Lambda ^\mathrm {op}$ triangle equivalences

$$\begin{aligned} {\mathbf {D}}^b({\text {mod }}\Lambda )^\mathrm {op}\xrightarrow {\ _\sim \ } {\mathbf {D}}^b(\widehat{{\text {fl }}\Gamma })\xrightarrow {\ _\sim \ }\widehat{{\mathbf {D}}^b({\text {fl }}\Gamma )}^b. \end{aligned}$$

This paper has three appendices. The first one by Tobias Barthel discusses completions for stable homotopy categories. In particular, we see that Theorem 1.1 generalises to ring spectra.

The second one by Tobias Barthel and Henning Krause refines for a separated noetherian scheme the description of the bounded derived category of coherent sheaves as a completion. It is shown that the objects are precisely the colimits of Cauchy sequences of perfect complexes that satisfy an intrinsic boundedness condition.

In the final appendix, Bernhard Keller introduces the notion of a morphic enhancement of a triangulated category, following [19]. This allows us to capture the notion of standard triangle and of coherent morphism between standard triangles, generalising analogous approaches via stable model categories or stable derivators. Morphic enhancements provide a setting for turning a completion into a triangulated category. In fact, we see that in Theorem 1.1 the completion of the morphic enhancement of ${\mathbf {D}}^\mathrm {per}(\Lambda )$ identifies with the morphic enhancement of ${\mathbf {D}}^b({\text {mod }}\Lambda )$.

After completion of this work, Neeman published a survey [36] which discusses metrics in triangulated categories, following work of Lawvere from the 1970s. Completing with respect to such metrics yields an alternative method of completing triangulated categories; it does not depend on an enhancement and we recommend a comparison.

2 The sequential completion of a category

Let ${\mathbb {N}}=\{0,1,2,\ldots \}$ denote the set of natural numbers, viewed as a category with a single morphism $i\rightarrow j$ if $i\le j$.

Now fix a category ${\mathcal {C}}$ and consider the category ${\text {Fun}}({\mathbb {N}},{\mathcal {C}})$ of functors ${\mathbb {N}}\rightarrow {\mathcal {C}}$. An object X is nothing but a sequence of morphisms $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {C}}$, and the morphisms between functors are by definition the natural transformations. We call X a Cauchy sequence if for all $C\in {\mathcal {C}}$ the induced map ${\text {Hom}}(C,X_i)\rightarrow {\text {Hom}}(C,X_{i+1})$ is invertible for $i\gg 0$. This means:

$$\begin{aligned} \forall \; C\in {\mathcal {C}}\;\; \exists \; n_C\in {\mathbb {N}}\;\; \forall \; j\ge i\ge n_C\;\; {\text {Hom}}(C,X_i)\xrightarrow {_\sim }{\text {Hom}}(C,X_j). \end{aligned}$$

Let ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$ denote the full subcategory consisting of all Cauchy sequences. A morphism $X\rightarrow Y$ is eventually invertible if for all $C\in {\mathcal {C}}$ the induced map ${\text {Hom}}(C,X_i)\rightarrow {\text {Hom}}(C,Y_i)$ is invertible for $i\gg 0$. This means:

$$\begin{aligned} \forall \; C\in {\mathcal {C}}\;\; \exists \; n_C\in {\mathbb {N}}\;\; \forall \; i\ge n_C\;\; {\text {Hom}}(C,X_i)\xrightarrow {_\sim }{\text {Hom}}(C,Y_i). \end{aligned}$$

Let S denote the class of eventually invertible morphisms in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$.

Definition 2.1

The sequential completion of ${\mathcal {C}}$ is the category

$$\begin{aligned} {\widehat{{\mathcal {C}}}}:= {\text {Cauch }}({\mathbb {N}},{\mathcal {C}})[S^{-1}] \end{aligned}$$

that is obtained from the Cauchy sequences by formally inverting all eventually invertible morphisms, together with the canonical functor ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ that sends an object X in ${\mathcal {C}}$ to the constant sequence $X\xrightarrow {{\text {id }}} X\xrightarrow {{\text {id }}} \cdots$.

A sequence $X:{\mathbb {N}}\rightarrow {\mathcal {C}}$ induces a functor

$$\begin{aligned} {\widetilde{X}}:{\mathcal {C}}^\mathrm {op}\longrightarrow \mathrm {Set},\quad C\mapsto \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(C,X_i), \end{aligned}$$

and this yields a functor

$$\begin{aligned} {\widehat{{\mathcal {C}}}}\longrightarrow {\text {Fun}}({\mathcal {C}}^\mathrm {op},\mathrm {Set}),\quad X\mapsto {\widetilde{X}}, \end{aligned}$$

because the assignment $X\mapsto {\widetilde{X}}$ maps eventually invertible morphisms to isomorphisms. We will show that this functor is fully faithful.

Let ${\mathcal {D}}$ be a category and S a class of morphisms in ${\mathcal {D}}$. There is an explicit description of the localisation ${\mathcal {D}}[S^{-1}]$ provided that the class S admits a calculus of left fractions in the sense of [12], that is, the following conditions are satisfied:

• (LF1) The identity morphism of each object is in S. The composition of two morphisms in S is again in S.

• (LF2) Each pair of morphisms $X'\xleftarrow {\sigma }X\rightarrow Y$ with $\sigma \in S$ can be completed to a commutative diagram

  

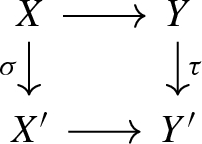
  such that $\tau \in S$.

• (LF3) Let $\alpha ,\beta :X\rightarrow Y$ be morphisms. If there is $\sigma :X'\rightarrow X$ in S such that $\alpha \sigma =\beta \sigma$, then there is $\tau :Y\rightarrow Y'$ in S such that $\tau \alpha =\tau \beta$.

If S admits a calculus of left fractions, then the morphisms in ${\mathcal {D}}[S^{-1}]$ are of the form $\sigma ^{-1}\alpha$ given by a pair of morphisms $X{\mathop {\rightarrow }\limits ^{\alpha }}Y'{\mathop {\leftarrow }\limits ^{\sigma }}Y$ in ${\mathcal {D}}$ with $\sigma \in S$, where we identify a morphism in ${\mathcal {D}}$ with its image under the canonical functor ${\mathcal {D}}\rightarrow {\mathcal {D}}[S^{-1}]$. For pairs $(\alpha _1,\sigma _1)$ and $(\alpha _2,\sigma _2)$ we have $\sigma _1^{-1}\alpha _1=\sigma _2^{-1}\alpha _2$ in ${\mathcal {D}}[S^{-1}]$ if and only if there exists a commutative diagram

with $\sigma$ in S; see [12].

Lemma 2.2

The eventually invertible morphisms in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$ admit a calculus of left fractions.

We need some preparations for the proof of this lemma. Given functors $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ and $X:{\mathbb {N}}\rightarrow {\mathcal {C}}$, let $X_f$ denote the composite $X\circ f$. Call f cofinal if $n\le f(n)$ for all $n\in {\mathbb {N}}$. In this case there is a natural morphism $f_X:X\rightarrow X_f$.

A straightforward computation of filtered colimits in $\mathrm {Set}$ yields the following.

Lemma 2.3

Let $X,Y:{\mathbb {N}}\rightarrow {\mathcal {C}}$ be functors.

• (1) Given a morphism $\phi :{\widetilde{X}}\rightarrow {\widetilde{Y}}$, there exists a cofinal $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ and a morphism $\alpha :X\rightarrow Y_f$ such that $\widetilde{f_Y}\phi ={\widetilde{\alpha }}$.

• (2) Given morphisms $\alpha ,\beta :X\rightarrow Y$ such that ${\widetilde{\alpha }}={\widetilde{\beta }}$, there exists a cofinal $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ such $f_Y\alpha =f_Y\beta$.

Proof

• (1) Fix $n\in {\mathbb {N}}$ and suppose f has been defined for all $m<n$. There exists $n'\ge \max (n, f(n-1))$ and $\alpha _n:X_n\rightarrow Y_{n'}$ such that the composite

  $$\begin{aligned} {\text {Hom}}(X_{n},X_{n})\rightarrow \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(X_n,X_i)\xrightarrow {\phi }\mathop {\mathrm{colim }}\limits _i{\text {Hom}}(X_n,Y_i) \end{aligned}$$

  maps ${\text {id }}_{X_n}$ to the image of $\alpha _n$ under ${\text {Hom}}(X_{n},Y_{n'})\rightarrow \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(X_n,Y_i)$. We set $f(n)=n'$ and can make this choice consistent such that the $\alpha _n$ yield a morphism $X\rightarrow Y_f$.

• (2) Fix $n\in {\mathbb {N}}$ and suppose f has been defined for all $m<n$. The fact that $\alpha$ and $\beta$ induce the same map $\mathop {\mathrm{colim }}\limits _i{\text {Hom}}(X_n,X_i)\rightarrow \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(X_n,Y_i)$ yields $n'\ge \max (n,f(n-1))$ such that ${\text {Hom}}(X_n,Y_n)\rightarrow {\text {Hom}}(X_n,Y_{n'})$ maps $\alpha _n$ and $\beta _n$ to the same element. Then set $f(n)=n'$.

$\square$

Let S denote the class of eventually invertible morphisms. If $X:{\mathbb {N}}\rightarrow {\mathcal {C}}$ is Cauchy and $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ is cofinal, then $X_f$ is Cauchy and the canonical morphism $f_X:X\rightarrow X_f$ is in S. Moreover, for any $\sigma :X\rightarrow Y$ in S there exists a cofinal $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ and a morphism $\sigma ':Y\rightarrow X_f$ such that $\sigma '\sigma =f_X$. This follows by applying Lemma 2.3 to ${{\widetilde{\sigma }}}^{-1}$.

Proof of Lemma 2.2

The condition (LF1) is clear. To check (LF2) fix a pair of morphisms $X'\xleftarrow {\sigma }X\xrightarrow {\alpha } Y$ with $\sigma \in S$. Choose $\sigma ':X'\rightarrow X_f$ such that $\sigma '\sigma =f_X$. Then we obtain the following commutative square with $f_Y\in S$.

To check (LF3) fix a pair of morphisms $\alpha ,\beta :X\rightarrow Y$. Let $\sigma :X'\rightarrow X$ in S such that $\alpha \sigma =\beta \sigma$. This implies ${\widetilde{\alpha }}={\widetilde{\beta }}$, and it follows from Lemma 2.3 that there exists a cofinal $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ such that $f_Y\alpha =f_Y\beta$. Note that $f_Y\in S$. $\square$

Proposition 2.4

The canonical functor ${\widehat{{\mathcal {C}}}}\rightarrow {\text {Fun}}({\mathcal {C}}^\mathrm {op},\mathrm {Set})$ is fully faithful; it identifies ${\widehat{{\mathcal {C}}}}$ with the colimits of sequences of representable functors that correspond to Cauchy sequences in ${\mathcal {C}}$. Also, the canonical functor ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ is fully faithful.

Proof

We use the fact that the class S of eventually invertible morphisms in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$ admits a calculus of left fractions. Then every morphism in ${\widehat{{\mathcal {C}}}}$ is of the form $\sigma ^{-1}\alpha$ given by a pair of morphisms $X\xrightarrow {\alpha }Y'\xleftarrow {\sigma } Y$ in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$ with $\sigma \in S$.

Fix Cauchy sequences $X,Y:{\mathbb {N}}\rightarrow {\mathcal {C}}$. We need to show that the canonical map

$$\begin{aligned} {\text {Hom}}(X,Y)\longrightarrow {\text {Hom}}({\widetilde{X}},{\widetilde{Y}}),\quad \sigma ^{-1}\alpha \mapsto {\widetilde{\sigma }}^{-1}{\widetilde{\alpha }}, \end{aligned}$$

is a bijection. The map is surjective, because Lemma 2.3 yields for any morphism $\phi :{\widetilde{X}}\rightarrow {\widetilde{Y}}$ a cofinal $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ and $\alpha :X\rightarrow Y_f$ such that $\phi =\widetilde{f_Y}^{-1}{\widetilde{\alpha }}$. Now fix a pair of morphisms $\sigma _1^{-1}\alpha _1$ and $\sigma _2^{-1}\alpha _2$ in ${\widehat{{\mathcal {C}}}}$ such that $\widetilde{\sigma _1}^{-1}\widetilde{\alpha _1}=\widetilde{\sigma _2}^{-1}\widetilde{\alpha _2}$. Use (LF2) to complete $\sigma _1$ and $\sigma _2$ to a commutative diagram

with $\tau _1,\tau _2\in S$. Then we have $\widetilde{\tau _1\alpha _1}=\widetilde{\tau _2\alpha _2}$ and there exists a cofinal $f:{\mathbb {N}}\rightarrow {\mathbb {N}}$ such that $f_Z\tau _1\alpha _1=f_Z\tau _2\alpha _2$. This implies $\sigma _1^{-1}\alpha _1=\sigma _2^{-1}\alpha _2$ in ${\widehat{{\mathcal {C}}}}$.

Colimits in ${\text {Fun}}({\mathcal {C}}^\mathrm {op},\mathrm {Set})$ are computed ‘pointwise’. Thus for X in ${\text {Fun}}({\mathbb {N}},{\mathcal {C}})$ the functor ${\widetilde{X}}$ is the colimit of the sequence

$$\begin{aligned} {\text {Hom}}(-,X_0)\rightarrow {\text {Hom}}(-,X_1)\rightarrow {\text {Hom}}(-,X_2)\rightarrow \cdots \end{aligned}$$

in ${\text {Fun}}({\mathcal {C}}^\mathrm {op},\mathrm {Set})$. It follows that ${\widehat{{\mathcal {C}}}}$ identifies with the colimits of sequences of representable functors that correspond to Cauchy sequences in ${\mathcal {C}}$.

Finally, the canonical functor ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ is fully faithful, since the composition with ${\widehat{{\mathcal {C}}}}\rightarrow {\text {Fun}}({\mathcal {C}}^\mathrm {op},\mathrm {Set})$ is fully faithful by Yoneda’s lemma. $\square$

Corollary 2.5

For $X,Y\in {\widehat{{\mathcal {C}}}}$ we have a natural bijection

$$\begin{aligned} {\text {Hom}}(X,Y)\xrightarrow {_\sim }\lim _i\mathop {\mathrm{colim }}\limits _j{\text {Hom}}(X_i,Y_j). \end{aligned}$$

Proof

Combining Proposition 2.4 and Yoneda’s lemma, we have

$$\begin{aligned} {\text {Hom}}(X,Y)&\cong {\text {Hom}}(\mathop {\mathrm{colim }}\limits _i{\text {Hom}}(-,X_i), \mathop {\mathrm{colim }}\limits _j{\text {Hom}}(-,Y_j))\\&\cong \lim _i{\text {Hom}}({\text {Hom}}(-,X_i), \mathop {\mathrm{colim }}\limits _j{\text {Hom}}(-,Y_j))\\&\cong \lim _i\mathop {\mathrm{colim }}\limits _j{\text {Hom}}(X_i,Y_j). \end{aligned}$$

$\square$

Call ${\mathcal {C}}$ sequentially complete if every Cauchy sequence in ${\mathcal {C}}$ has a colimit in ${\mathcal {C}}$. Clearly, ${\mathcal {C}}$ is sequentially complete if and only if the canonical functor ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ is an equivalence. We do not know whether ${\widehat{{\mathcal {C}}}}$ is always sequentially complete.

Remark 2.6

From Proposition 2.4 it follows that the sequential completion of ${\mathcal {C}}$ identifies with a full subcategory of the ind-completion ${\text {Ind }}({\mathcal {C}})$ in the sense of [14, Sect. 8].

Remark 2.7

Let $F:{\mathcal {C}}\rightarrow {\mathcal {D}}$ be a functor.

• (1) Suppose that F admits a left adjoint. Then F preserves Cauchy sequences and induces therefore a functor $\widehat{F}:{\widehat{{\mathcal {C}}}}\rightarrow {\widehat{{\mathcal {D}}}}$ such that

  $$\begin{aligned} {\widehat{F}}(X)=\mathop {\mathrm{colim }}\limits _iF(X_i) \quad \text {for} \quad X\in {\widehat{C}}. \end{aligned}$$

  (2.1)

• (2) Suppose that ${\mathcal {D}}$ admits filtered colimits. Then F extends via (2.1) to a functor ${\widehat{{\mathcal {C}}}}\rightarrow {\mathcal {D}}$.

• (3) If (F, G) is an adjoint pair of functors that preserve Cauchy sequences, then $({\widehat{F}},{\widehat{G}})$ is an adjoint pair since

  $$\begin{aligned} {\text {Hom}}({\widehat{F}}(X),Y)&\cong {\text {Hom}}(\mathop {\mathrm{colim }}\limits _iF(X_i), \mathop {\mathrm{colim }}\limits _j Y_j)\\&\cong \lim _i\mathop {\mathrm{colim }}\limits _j{\text {Hom}}(F(X_i),Y_j)\\&\cong \lim _i\mathop {\mathrm{colim }}\limits _j{\text {Hom}}(X_i,G(Y_j))\\&\cong {\text {Hom}}(X,{\widehat{G}}(Y)). \end{aligned}$$

The notion of a Cauchy sequence goes back to work of Bolzano and Cauchy (providing a criterion for convergence), while the construction of the real numbers from the rationals via equivalence classes of Cauchy sequences is due to Cantor and Méray [5, 27]. The sequential completion generalises this construction.

Example 2.8

View the rational numbers ${\mathbb {Q}}=({\mathbb {Q}},\le )$ with the usual ordering as a category and let ${\mathbb {R}}_\infty =({\mathbb {R}}\cup \{\infty \},\le )$. Taking a Cauchy sequence to its limit yields a functor

For $x\in {\mathbb {R}}_\infty$, there are precisely two isomorphism classes of objects in ${\widehat{{\mathbb {Q}}}}$ with limit x when x is rational (depending on whether the sequence is eventually constant or not); otherwise there is precisely one isomorphism class in ${\widehat{{\mathbb {Q}}}}$ with limit x.¹

Proof

A Cauchy sequence $x\in {\text {Cauch }}({\mathbb {N}},{\mathbb {Q}})$ is by definition a sequence $x_0\le x_1\le x_2\le \cdots$ of rational numbers that is either bounded, so converges to ${\bar{x}}\in {\mathbb {R}}$, or it is unbounded and we set ${\bar{x}}=\infty$. Given a morphism $x\rightarrow y$ in ${\text {Cauch }}({\mathbb {N}},{\mathbb {Q}})$ that is eventually invertible, we have ${\bar{x}}={\bar{y}}$. Conversely, if ${\bar{x}}={\bar{y}}$, then we define $u\in {\text {Cauch }}({\mathbb {N}},{\mathbb {Q}})$ by $u_i={\text {min }}(x_i,y_i)$ and have morphisms $x\leftarrow u\rightarrow y$. It is easily checked that $u\rightarrow x$ is eventually invertible, except when x is eventually constant and y is not. Thus the assignment $x\mapsto {\bar{x}}$ yields the desired functor ${\widehat{{\mathbb {Q}}}}\twoheadrightarrow {\mathbb {R}}_\infty$. $\square$

Let ${\mathbb {I}}=\{0<1\}$ denote the poset consisting of two elements. For any category ${\mathcal {C}}$, the category of morphisms in ${\mathcal {C}}$ identifies with ${\mathcal {C}}^{{\mathbb {I}}}={\text {Fun}}({\mathbb {I}},{\mathcal {C}})$.

Example 2.9

Let ${\mathcal {C}}$ be a category that admits an initial object and set ${\mathcal {D}}={\mathcal {C}}^{\mathbb {I}}$. Then there is a canonical equivalence ${\widehat{{\mathcal {C}}}}^{\mathbb {I}}\xrightarrow {_\sim }\widehat{{\mathcal {D}}}$.

Proof

The equivalence

$$\begin{aligned} F:{\text {Fun}}({\mathbb {I}},{\text {Fun}}({\mathbb {N}},{\mathcal {C}}))\xrightarrow {_\sim }{\text {Fun}}({\mathbb {I}}\times {\mathbb {N}},{\mathcal {C}}) \xrightarrow {_\sim }{\text {Fun}}({\mathbb {N}},{\text {Fun}}({\mathbb {I}},{\mathcal {C}})) \end{aligned}$$

restricts to an equivalence

$$\begin{aligned} F_0:{\text {Fun}}({\mathbb {I}},{\text {Cauch }}({\mathbb {N}},{\mathcal {C}})) \xrightarrow {_\sim }{\text {Cauch }}({\mathbb {N}},{\text {Fun}}({\mathbb {I}},{\mathcal {C}})). \end{aligned}$$

In order to see this, let $\phi :X\rightarrow Y$ be a morphism in ${\text {Fun}}({\mathbb {N}},{\mathcal {C}})$ and $\alpha :C\rightarrow D$ a morphism in ${\mathcal {C}}$. Suppose X and Y are in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$. Thus there is $n\in {\mathbb {N}}$ such that ${\text {Hom}}(C,X_i)\xrightarrow {_\sim }{\text {Hom}}(C,X_{i+1})$ and ${\text {Hom}}(D,Y_i)\xrightarrow {_\sim }{\text {Hom}}(D,Y_{i+1})$ for $i\ge n$. Then ${\text {Hom}}(\alpha ,\phi _i)\xrightarrow {_\sim }{\text {Hom}}(\alpha ,\phi _{i+1})$ for $i\ge n$. Thus $F(\phi )$ is in ${\text {Cauch }}({\mathbb {N}},{\text {Fun}}({\mathbb {I}},{\mathcal {C}}))$. On the other hand, if $F(\phi )$ is in ${\text {Cauch }}({\mathbb {N}},{\text {Fun}}({\mathbb {I}},{\mathcal {C}}))$, then we choose $\alpha ={\text {id }}_C$ and $\alpha :I\rightarrow D$ (I the initial object in ${\mathcal {C}}$) to see that X and Y are in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$. It is easily checked that $F_0$ induces a functor ${\widehat{{\mathcal {C}}}}^{\mathbb {I}}\rightarrow \widehat{{\mathcal {C}}^{\mathbb {I}}}$, and we claim that it is an equivalence. Recall from Remark 2.6 that there is a canonical embedding ${\widehat{{\mathcal {C}}}}\rightarrow {\text {Ind }}({\mathcal {C}})$. So it remains to use the fact that ${\text {Ind }}({\mathcal {C}})^{\mathbb {I}}\xrightarrow {_\sim }{\text {Ind }}({\mathcal {C}}^{\mathbb {I}})$, which follows from Propositions 8.8.2 and 8.8.5 in [14]. $\square$

Let us generalise the definition of the completion ${\widehat{{\mathcal {C}}}}$, because later on we need to modify the underlying choice of Cauchy sequences. We fix a class ${\mathcal {X}}$ of objects in ${\text {Fun}}({\mathbb {N}},{\mathcal {C}})$. The completion of ${\mathcal {C}}$ with respect to ${\mathcal {X}}$ is the category $\widehat{{\mathcal {C}}_{\mathcal {X}}}$ with class of objects ${\mathcal {X}}$ and

$$\begin{aligned} {\text {Hom}}(X,Y)=\lim _i\mathop {\mathrm{colim }}\limits _j{\text {Hom}}(X_i,Y_j)\quad \text {for}\quad X,Y\in {\mathcal {X}}. \end{aligned}$$

It follows from the definition that the assignment $X\mapsto \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(-,X_i)$ induces a fully faithful functor $\widehat{{\mathcal {C}}_{\mathcal {X}}}\rightarrow {\text {Fun}}({\mathcal {C}}^\mathrm {op},\mathrm {Set})$. Clearly, $\widehat{{\mathcal {C}}}$ identifies with $\widehat{{\mathcal {C}}_{\mathcal {X}}}$ when ${\mathcal {X}}$ equals the class of Cauchy sequences, by Corollary 2.5.

Example 2.10

Let ${\mathcal {C}}$ be an exact category and let ${\mathcal {X}}$ denote the class of sequences X such that each $X_i\rightarrow X_{i+1}$ is an admissible monomorphism. Then ${\mathcal {C}}\tilde{\,}:=\widehat{{\mathcal {C}}_{\mathcal {X}}}$ admits a canonical exact structure and is called countable envelope of ${\mathcal {C}}$ [18, Appendix B].

3 The sequential completion of an abelian category

Let ${\mathcal {C}}$ be an additive category.

Lemma 3.1

The sequential completion ${\widehat{{\mathcal {C}}}}$ is an additive category and the canonical functor ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ is additive.

Proof

The assertion follows from the fact that ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$ is additive and that the eventually invertible morphisms admit a calculus of left fractions [12, I.3.3]. $\square$

It follows that the assignment $X\mapsto {\widetilde{X}}$ yields a fully faithful additive functor ${\widehat{{\mathcal {C}}}}\rightarrow {\text {Add }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab})$ into the category of additive functors ${\mathcal {C}}^\mathrm {op}\rightarrow \mathrm {Ab}$.

Lemma 3.2

If ${\mathcal {C}}$ admits kernels, then ${\widehat{{\mathcal {C}}}}$ admits kernels and ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ is left exact.

Proof

A morphism $X\rightarrow Y$ in ${\widehat{{\mathcal {C}}}}$ is up to isomorphism given by a morphism $\phi :X\rightarrow Y$ in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$. Then $K:=({\text {Ker }}\phi _i)_{i\ge 0}$ is a Cauchy sequence, and this yields the kernel in ${\widehat{{\mathcal {C}}}}$, because the sequence $0\rightarrow \widetilde{K}\rightarrow {\widetilde{X}} \rightarrow {\widetilde{Y}}$ is exact in ${\text {Add }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab})$. $\square$

Let ${\mathcal {A}}$ be an abelian category. We write ${\text {fl }}{\mathcal {A}}$ for the full subcategory of objects having finite composition length, and ${\text {art }}{\mathcal {A}}$ denotes the full subcategory of artinian objects. For $X\in {\mathcal {A}}$ the socle ${\text {soc }}X$ is the sum of all simple subobjects. One defines inductively ${\text {soc }}^n X\subseteq X$ for $n\ge 0$ by setting ${\text {soc }}^0 X=0$, and ${\text {soc }}^{n+1}X$ is given by the exact sequence

$$\begin{aligned} 0\longrightarrow {\text {soc }}^n X\longrightarrow {\text {soc }}^{n+1} X\longrightarrow {\text {soc }}(X/{\text {soc }}^n X)\longrightarrow 0. \end{aligned}$$

Example 3.3

Let ${\mathcal {A}}={\text {Mod }}\Lambda$ be the module category of a commutative noetherian local ring $\Lambda$. Then the sequential completion of ${\text {fl }}{\mathcal {A}}$ identifies with ${\text {art }}{\mathcal {A}}$.

Proof

Set ${\mathcal {C}}={\text {fl }}{\mathcal {A}}$. It is well known that a $\Lambda$-module X is artinian if and only if its socle has finite length. In that case the socle series $({\text {soc }}^iX)_{i\ge 0}$ of X yields a Cauchy sequence in ${\mathcal {C}}$ with $\mathop {\mathrm{colim }}\limits _i({\text {soc }}^iX)=X$.

Now let $X\in {\widehat{{\mathcal {C}}}}$. The assignment $X\mapsto {\bar{X}}:=\mathop {\mathrm{colim }}\limits _i X_i$ yields a fully faithful functor ${\widehat{{\mathcal {C}}}}\rightarrow {\mathcal {A}}$. Let S denote the unique (up to isomorphism) simple object in ${\mathcal {A}}$. Then ${\text {soc }}{\bar{X}}$ has finite length, since ${\text {soc }}{\bar{X}}\cong {\text {Hom}}(S,\bar{X})\cong \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(S, X_i)$. Thus ${\bar{X}}$ is artinian. $\square$

The preceding example suggests a general criterion such that the sequential completion of an abelian category is abelian.

Let us fix a length category ${\mathcal {C}}$. Thus ${\mathcal {C}}$ is an abelian category and every object has finite length. We call ${\mathcal {C}}$ ind-artinian if

• (1) ${\mathcal {C}}$ has only finitely many isomorphism classes of simple objects,

• (2) ${\mathcal {C}}$ is right Ext-finite, that is, for every pair of simple objects S and T the ${\text {End }}(S)$-module ${\text {Ext }}^1(S,T)$ has finite length, and

• (3) ${\mathcal {C}}$ satisfies the descending chain condition on subobjects of socle stable sequences in ${\mathcal {C}}$.

Here, we consider sequences $X=(X_i\rightarrow X_{i+1})_{i\ge 0}$ of morphisms in ${\mathcal {C}}$, so functors $({\mathbb {N}},\le )\rightarrow {\mathcal {C}}$, and X is socle stable if $X_i\xrightarrow {\sim } {\text {soc }}^i X_j$ for all $j\ge i$. A subobject $X\subseteq Y$ is given by a morphism of functors $X\rightarrow Y$ such that $X_i\rightarrow Y_i$ is a monomorphism for all $i\ge 0$.

Proposition 3.4

Let ${\mathcal {A}}$ be a Grothendieck category with a fully faithful functor ${\mathcal {C}}\hookrightarrow {\mathcal {A}}$ that identifies ${\mathcal {C}}$ with the full subcategory of finite length objects in ${\mathcal {A}}$. Suppose that every object in ${\mathcal {A}}$ is the union of its finite length subobjects. Then the following are equivalent:

• (1) The category ${\mathcal {C}}$ is ind-artinian.

• (2) The category ${\mathcal {C}}$ has only finitely many isomorphism classes of simple objects, and an object in ${\mathcal {A}}$ is artinian if its socle has finite length.

• (3) The category ${\mathcal {A}}$ admits an artinian cogenerator.

In this case an object in ${\mathcal {A}}$ is artinian if and only if it is the colimit of a Cauchy sequence in ${\mathcal {C}}$.

Proof

Let us begin with the observation that for every artinian object $X\in {\mathcal {A}}$ the socle series $({\text {soc }}^i X)_{i\ge 0}$ is a Cauchy sequence in ${\mathcal {C}}$ with colimit X. To see this, note that $X_i:={\text {soc }}^i X\in {\mathcal {C}}$ for all i since $X_i/X_{i-1}$ is semisimple and artinian, so of finite length. Furthermore, each object $C\in {\mathcal {C}}$ satisfies ${\text {soc }}^nC=C$ for some n, and then every morphism $C\rightarrow X$ factors through $X_n$. Thus ${\text {Hom}}(C,X_i)\xrightarrow {_\sim }{\text {Hom}}(C,X_{i+1})$ for all $i\ge n$, and $X=\bigcup _i{\text {soc }}^i X$.

(1) $\Rightarrow$ (2): Let $X\in {\mathcal {A}}$ and suppose that ${\text {soc }}X$ has finite length. An injective envelope $X\rightarrow E$ induces an isomorphism ${\text {soc }}X\xrightarrow {_\sim }{\text {soc }}E$. So we may assume that X is injective. Set $X_i:={\text {soc }}^iX$ for $i\ge 0$. The assumption on ${\mathcal {C}}$ implies that $X_n$ has finite length for all $n > 0$. This follows by induction from the defining exact sequence for ${\text {soc }}^n$ as follows. Let $S=\bigoplus _i S_i$ be the direct sum of a representative set of simple objects. For $n>0$ we have an isomorphism of ${\text {End }}(S)$-modules

$$\begin{aligned} {\text {Hom}}(S,X/X_n)\cong {\text {Ext }}^1(S,X_n), \end{aligned}$$

and their length equals the length of ${\text {soc }}(X/X_n)$. Thus $X_n\in {\mathcal {C}}$ for all $n>0$.

The sequence $(X_i\rightarrow X_{i+1})_{i\ge 0}$ is socle stable, and the subobjects $U\subseteq X$ identify with subobjects of this socle stable sequence by taking U to the sequence $(U_i\rightarrow U_{i+1})_{i\ge 0}$ given by $U_i:={\text {soc }}^iU=U\cap X_i$. The inverse map takes a subsequence $(V_i\rightarrow V_{i+1})_{i\ge 0}$ given by subobjects $V_i\subseteq X_i$ to $\bigcup _iV_i\subseteq X$. Thus X is artinian.

(2) $\Rightarrow$ (3): Choose an injective envelope $E=E(S)$ in ${\mathcal {A}}$ for the direct sum $S=\bigoplus _i S_i$ of a representative set of simple objects. Then E is an injective cogenerator which is artinian since ${\text {soc }}E\cong S$.

(3) $\Rightarrow$ (1): Choose an artinian cogenerator E of ${\mathcal {A}}$, and we may assume E is injective since for each simple S the injective envelope E(S) is a direct summand of E. The number of isoclasses of simple objects is bounded by the length of ${\text {soc }}E$ and is therefore finite. Fix simple objects $S,T\in {\mathcal {A}}$ and choose a monomorphism $T\rightarrow E$. Then ${\text {Hom}}(S,E/T)\cong {\text {Ext }}^1(S,T)$ and the length of ${\text {Ext }}^1(S,T)$ as ${\text {End }}(S)$-module is bounded by the length of ${\text {soc }}(E/T)$ which is finite since E/T is artinian. It follows that ${\mathcal {C}}$ is right ext-finite. Now fix a socle stable sequence $(X_i\rightarrow X_{i+1})_{i\ge 0}$ in ${\mathcal {C}}$ and set $X=\mathop {\mathrm{colim }}\limits _i X_i$. Note that $X_i\cong {\text {soc }}^iX$ for all $i\ge 0$. Then X embeds into the injective envelope $E(X_1)$ and is therefore artinian. Subobjects of $(X_i\rightarrow X_{i+1})_{i\ge 0}$ correspond to subobjects of X by the first part of the proof. Thus ${\mathcal {C}}$ is ind-artinian.

It remains to establish the last assertion. We have already seen that any artinian object is the colimit of a Cauchy sequence in ${\mathcal {C}}$. Conversely, let $X\in {\mathcal {A}}$ be the colimit of a Cauchy sequence $(X_i)_{i\ge 0}$ in ${\mathcal {C}}$ and let $n\in {\mathbb {N}}$ such that for every simple object S we have ${\text {Hom}}(S,X_i)\xrightarrow {_\sim }{\text {Hom}}(S,X_{i+1})$ for all $i\ge n$. Then ${\text {soc }}X={\text {soc }}X_n$ is in ${\mathcal {C}}$, and therefore X is artinian. $\square$

Recall that an abelian category satisfies the (AB5) condition if for every directed set of subobjects $(A_i)_{i\in I}$ of an object A and $B\subseteq A$ one has

$$\begin{aligned} \left( \sum _{i\in I}A_i\right) \cap B=\sum _{i\in I}(A_i\cap B). \end{aligned}$$

Corollary 3.5

Let ${\mathcal {C}}$ be a length category and suppose ${\mathcal {C}}$ is ind-artinian. Then ${\widehat{{\mathcal {C}}}}$ is an abelian category with injective envelopes, satisfying the (AB5) condition, and every object is artinian. Moreover, the canonical functor ${\mathcal {C}}\rightarrow {\widehat{{\mathcal {C}}}}$ induces an equivalence ${\mathcal {C}}\xrightarrow {_\sim }{\text {fl }}{\widehat{{\mathcal {C}}}}$.

Proof

We embed ${\mathcal {C}}$ into a Grothendieck category via the functor

$$\begin{aligned} {\mathcal {C}}\longrightarrow {\mathcal {A}}:={\text {Lex }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab}),\quad X\mapsto {\text {Hom}}(-,X), \end{aligned}$$

where ${\text {Lex }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab})$ denotes the category of left exact functors ${\mathcal {C}}^\mathrm {op}\rightarrow \mathrm {Ab}$; see [11]. Then ${\widehat{{\mathcal {C}}}}$ identifies with a subcategory of ${\mathcal {A}}$ via Proposition 2.4, and Proposition 3.4 implies that ${\widehat{{\mathcal {C}}}}={\text {art }}{\mathcal {A}}$. From this the assertion follows. $\square$

Example 3.6

Let $\Lambda$ be a noetherian algebra over a complete local ring and set ${\mathcal {A}}={\text {Mod }}\Lambda$. Then ${\text {fl }}{\mathcal {A}}$ is ind-artinian and $\widehat{{\text {fl }}{\mathcal {A}}}$ identifies with ${\text {art }}{\mathcal {A}}$.

Proof

There are only finite many simple $\Lambda$-modules, up to isomorphism, and their injective envelopes are artinian. Thus ${\text {fl }}{\mathcal {A}}$ is ind-artinian by Proposition 3.4, and therefore $\widehat{{\text {fl }}{\mathcal {A}}}$ identifies with ${\text {art }}{\mathcal {A}}$. $\square$

Example 3.7

Let $\Lambda$ be a ring and ${\mathcal {C}}\subseteq {\text {Mod }}\Lambda$ a full subcategory of its module category that contains $\Lambda$. Then ${\mathcal {C}}$ is sequentially complete.

Proof

Let $X\in {\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$. We have ${\text {Hom}}(\Lambda ,X_i)\cong X_i$, and therefore $X_i\xrightarrow {_\sim }X_{i+1}$ for $i\gg 0$. Thus $\mathop \mathrm{colim}\nolimits _i X_i$ belongs to ${\mathcal {C}}$. $\square$

4 The sequential completion of a triangulated category

Let ${\mathcal {T}}$ be a triangulated category and suppose that countable coproducts exist in ${\mathcal {T}}$. Let

be a sequence of morphisms in ${\mathcal {T}}$. A homotopy colimit of this sequence is by definition an object X that occurs in an exact triangle

We write $\mathop {\mathrm{hocolim }}\limits _i X_i$ for X and observe that a homotopy colimit is unique up to a (non-unique) isomorphism [2].

Recall that an object C in ${\mathcal {T}}$ is compact if ${\text {Hom}}(C,-)$ preserves all coproducts. A morphism $X\rightarrow Y$ is phantom if any composition $C\rightarrow X\rightarrow Y$ with C compact is zero [6, 7]. The phantom morphisms form an ideal and we write ${\text {Ph }}(X,Y)$ for the subgroup of all phantoms in ${\text {Hom}}(X,Y)$. Let us denote by ${\mathcal {T}}/{\text {Ph }}$ the additive category which is obtained from ${\mathcal {T}}$ by annihilating all phantom morphisms.

Lemma 4.1

Let $C\in {\mathcal {T}}$ be compact. Any sequence $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {T}}$ induces an isomorphism

$$\begin{aligned} \mathop {\mathrm{colim }}\limits _i{\text {Hom}}(C,X_i)\xrightarrow {\ _\sim \ }{\text {Hom}}(C,\mathop {\mathrm{hocolim }}\limits _i X_i). \end{aligned}$$

Proof

See [20, Sect. 5.1] or [30, Lemma 1.5]. $\square$

Recall that for any sequence $\cdots \rightarrow A_2\xrightarrow {\phi _2} A_1\xrightarrow {\phi _1} A_0$ of maps between abelian groups the inverse limit and its first derived functor are given by the exact sequence

The following result goes back to work of Milnor [28] and was later extended by several authors, for instance in [6, 7].

Lemma 4.2

Let $X=\mathop {\mathrm{hocolim }}\limits _i X_i$ be a homotopy colimit in ${\mathcal {T}}$ such that each $X_i$ is a coproduct of compact objects. Then we have for any Y in ${\mathcal {T}}$ a natural exact sequence

$$\begin{aligned} 0\longrightarrow {\text {Ph }}(X,Y)\longrightarrow {\text {Hom}}(X,Y)\longrightarrow \lim _i{\text {Hom}}(X_i,Y)\longrightarrow 0 \end{aligned}$$

and an isomorphism

Proof

Apply ${\text {Hom}}(-,Y)$ to the exact triangle defining $\mathop {\mathrm{hocolim }}\limits _i X_i$ and use that a morphism $X\rightarrow Y$ is phantom if and only if it factors through the canonical morphism $X\rightarrow \coprod _{i\ge 0}\Sigma X_i$. $\square$

Let ${\mathcal {C}}\subseteq {\mathcal {T}}$ be a full additive subcategory consisting of compact objects and consider the restricted Yoneda functor

$$\begin{aligned} {\mathcal {T}}\longrightarrow {\text {Add }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab}),\quad X\mapsto h_X:={\text {Hom}}(-,X)|_{\mathcal {C}}. \end{aligned}$$

Note that for any sequence $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {C}}$ we have by Lemma 4.1

$$\begin{aligned} {\widetilde{X}}=\mathop {\mathrm{colim }}\limits _i{\text {Hom}}(-,X_i)=h_{\mathop {\mathrm{hocolim }}\limits _i X_i}. \end{aligned}$$

(4.1)

Lemma 4.3

Let $X=\mathop {\mathrm{hocolim }}\limits _i X_i$ be a homotopy colimit in ${\mathcal {T}}$ such that each $X_i$ is a coproduct of objects in ${\mathcal {C}}$. Then we have for any Y in ${\mathcal {T}}$ a natural isomorphism

$$\begin{aligned} \frac{{\text {Hom}}(X,Y)}{{\text {Ph }}(X,Y)}\xrightarrow {\ _\sim \ }{\text {Hom}}(h_X,h_Y). \end{aligned}$$

Proof

Using the preceding lemmas, we have

$$\begin{aligned} \frac{{\text {Hom}}(X,Y)}{{\text {Ph }}(X,Y)}&\cong \lim _i{\text {Hom}}(X_i,Y)\\&\cong \lim _i{\text {Hom}}(h_{X_i},h_{Y})\\&\cong {\text {Hom}}(\mathop {\mathrm{colim }}\limits _ih_{X_i},h_{Y})\\&\cong {\text {Hom}}(h_X,h_Y). \end{aligned}$$

$\square$

Proposition 4.4

Let ${\mathcal {C}}\subseteq {\mathcal {T}}$ be a full additive subcategory consisting of compact objects. Taking a sequence $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {C}}$ to its homotopy colimit induces a fully faithful functor $\widehat{{\mathcal {C}}}\rightarrow {\mathcal {T}}/{\text {Ph }}$.

Proof

We have the functor

$$\begin{aligned} {\widehat{{\mathcal {C}}}}\longrightarrow {\text {Add }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab}),\quad X\mapsto {\widetilde{X}}, \end{aligned}$$

which is fully faithful by Proposition 2.4. Now combine (4.1) and Lemma 4.3. $\square$

Definition 4.5

Let ${\mathcal {C}}$ be a triangulated category and ${\mathcal {X}}$ a class of sequences $(X_i)_{i\ge 0}$ in ${\mathcal {C}}$ that is stable under suspensions, i.e. $(\Sigma ^nX_i)_{i\ge 0}$ is in ${\mathcal {X}}$ for all $n\in {\mathbb {Z}}$. We say that ${\mathcal {X}}$ is phantomless if for any pair of sequences X, Y in ${\mathcal {X}}$ we have

(4.2)

The following lemma justifies the term ‘phantomless’.

Lemma 4.6

Let ${\mathcal {C}}\subseteq {\mathcal {T}}$ be a full triangulated subcategory consisting of compact objects and ${\mathcal {X}}$ a class of sequences $(X_i)_{i\ge 0}$ in ${\mathcal {C}}$ that is stable under suspensions. Consider the full subcategory

$$\begin{aligned} {\mathcal {D}}:=\{\mathop {\mathrm{hocolim }}\limits _i X_i\in {\mathcal {T}}\mid X\in {\mathcal {X}}\}\subseteq {\mathcal {T}}. \end{aligned}$$

Then the following are equivalent:

• (1) The class ${\mathcal {X}}$ is phantomless.

• (2) We have ${\text {Ph }}(U,V)=0$ for all $U,V\in {\mathcal {D}}$.

• (3) The functor ${\mathcal {D}}\rightarrow {\text {Add }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab})$ taking X to ${\text {Hom}}(-,X)|_{\mathcal {C}}$ is fully faithful.

• (4) The assignment $X\mapsto \mathop {\mathrm{hocolim }}\limits _i X_i$ yields an equivalence $\widehat{{\mathcal {C}}_{\mathcal {X}}}\xrightarrow {_\sim }{\mathcal {D}}$.

In this case the homotopy colimit of a Cauchy sequence in ${\mathcal {C}}$ is actually a colimit in ${\mathcal {D}}$, provided that ${\mathcal {X}}$ contains all constant sequences consisting of identities only.

Proof

(1) $\Leftrightarrow$ (2): Combine Lemmas 4.1 and 4.2.

(2) $\Leftrightarrow$ (3): Apply Lemma 4.3.

(2) $\Leftrightarrow$ (4): Apply Proposition 4.4.

The final assertion follows from the identity (4.1) for any sequence X in ${\mathcal {C}}$, since ${\mathcal {D}}$ identifies with a full subcategory of ${\text {Add }}({\mathcal {C}}^\mathrm {op},\mathrm {Ab})$. $\square$

Recall that a triangulated category is algebraic if it is triangle equivalent to the stable category ${\text {St }}({\mathcal {A}})$ of a Frobenius category ${\mathcal {A}}$. A morphism between exact triangles

in ${\text {St }}({\mathcal {A}})$ will be called coherent if it can be lifted to a morphism

between exact sequences in ${\mathcal {A}}$ (so that the canonical functor ${\mathcal {A}}\rightarrow {\text {St }}({\mathcal {A}})$ maps the second to the first diagram). Note that any commutative diagram

in ${\text {St }}({\mathcal {A}})$ can be completed to a coherent morphism of exact triangles as above.

The following theorem establishes a triangulated structure for the sequential completion of a triangulated category ${\mathcal {C}}$. Let us stress that we use a relative version of this result for our applications, as explained in Remark 4.10 below; it depends on the choice of a class ${\mathcal {X}}$ of sequences in ${\mathcal {C}}$ which is phantomless.

Theorem 4.7

Let ${\mathcal {C}}$ be an algebraic triangulated category, viewed as a full subcategory of its sequential completion ${\widehat{{\mathcal {C}}}}$. Suppose that the class of Cauchy sequences is phantomless. Then ${\widehat{{\mathcal {C}}}}$ admits a unique triangulated structure such that the exact triangles are precisely the ones isomorphic to colimits of Cauchy sequences that are given by coherent morphisms of exact triangles in ${\mathcal {C}}$.

Let us spell out the triangulated structure for ${\widehat{{\mathcal {C}}}}$. Fix a sequence of coherent morphisms $\eta _0\rightarrow \eta _1\rightarrow \eta _2\rightarrow \cdots$ of exact triangles

$$\begin{aligned} \eta _i:X_i\longrightarrow Y_i\longrightarrow Z_i\longrightarrow \Sigma X_i \end{aligned}$$

in ${\mathcal {C}}$ and suppose that it is also a sequence of morphisms $X\rightarrow Y\rightarrow Z\rightarrow \Sigma X$ of Cauchy sequences in ${\mathcal {C}}$. This identifies with the sequence

$$\begin{aligned} \mathop {\mathrm{colim }}\limits _i X_i \longrightarrow \mathop {\mathrm{colim }}\limits _i Y_i\longrightarrow \mathop {\mathrm{colim }}\limits _i Z_i\longrightarrow \mathop {\mathrm{colim }}\limits _i\Sigma X_i \end{aligned}$$

in ${\widehat{{\mathcal {C}}}}$, and the exact triangles in ${\widehat{{\mathcal {C}}}}$ are precisely sequences of morphisms that are isomorphic to sequences of the above form.

Theorem C.8 provides a substantial generalisation, from algebraic triangulated categories to triangulated categories with a morphic enhancement. Moreover, in some interesting cases the morphic enhancement extends to a morphic enhancement of the completion; see Sect. C.8.

Proof

The proof is given in several steps.

• (1) The assumption on ${\mathcal {C}}$ to be algebraic implies that ${\mathcal {C}}$ identifies with the stable category ${\text {St }}({\mathcal {A}})$ of a Frobenius category ${\mathcal {A}}$. Let ${\mathcal {A}}\tilde{\,}$ denote the countable envelope of ${\mathcal {A}}$ which is a Frobenius category containing ${\mathcal {A}}$ as a full exact subcategory; see Example 2.10. Then ${\mathcal {C}}$ identifies with a full triangulated subcategory of compact objects of ${\mathcal {T}}:={\text {St }}({\mathcal {A}}\tilde{\,})$. For any sequence of coherent morphisms $\eta _0\rightarrow \eta _1\rightarrow \eta _2\rightarrow \cdots$ of exact triangles

  $$\begin{aligned} \eta _i:X_i\longrightarrow Y_i\longrightarrow Z_i\longrightarrow \Sigma X_i \end{aligned}$$

  in ${\mathcal {C}}$ there is in ${\mathcal {T}}$ an induced exact triangle

  $$\begin{aligned} \mathop {\mathrm{hocolim }}\limits _i X_i\longrightarrow \mathop {\mathrm{hocolim }}\limits _i Y_i\longrightarrow \mathop {\mathrm{hocolim }}\limits _i Z_i\longrightarrow \Sigma (\mathop {\mathrm{hocolim }}\limits _i X_i). \end{aligned}$$

  (4.3)

  Let us sketch the argument. We can lift the sequence $(\eta _i)_{i\ge 0}$ to a sequence of exact sequences

  $$\begin{aligned} {\tilde{\eta }}_i:0\longrightarrow {\tilde{X}}_i\longrightarrow {\tilde{Y}}_i\longrightarrow \tilde{Z}_i\longrightarrow 0 \end{aligned}$$

  in ${\mathcal {A}}$ and obtain a commutative diagram with exact rows

  

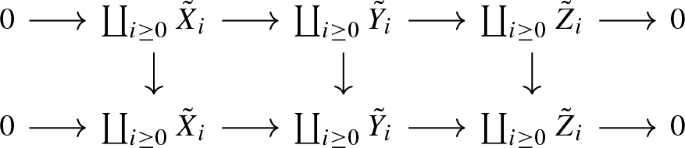
  in ${\mathcal {A}}\tilde{\,}$. The vertical morphism are induced by the morphisms ${\tilde{\eta }}_i\rightarrow {\tilde{\eta }}_{i+1}$, and taking mapping cones of the vertical morphisms (given by cokernels in ${\mathcal {A}}\tilde{\,}$) yields the desired exact triangle (4.3).

• (2) The assumption on Cauchy sequences in ${\mathcal {C}}$ to be phantomless implies that the functor ${\widehat{{\mathcal {C}}}}\rightarrow {\mathcal {T}}$ taking a sequence to its homotopy colimit induces an equivalence

  $$\begin{aligned} {\widehat{{\mathcal {C}}}}\xrightarrow {\ _\sim \ }{\mathcal {D}}:=\{\mathop {\mathrm{hocolim }}\limits _i X_i\in {\mathcal {T}}\mid X\in {\text {Cauch }}({\mathbb {N}},{\mathcal {C}})\}. \end{aligned}$$

  This follows from Lemma 4.6. In particular, the homotopy colimit of a Cauchy sequence in ${\mathcal {C}}$ is actually a colimit in ${\mathcal {D}}$.

• (3) We claim that ${\mathcal {D}}$ is a triangulated subcategory of ${\mathcal {T}}$ and that the exact triangles in ${\mathcal {D}}$ are up to isomorphism the colimits of Cauchy sequences given by coherent morphisms of exact triangles in ${\mathcal {C}}$. For a Cauchy sequence given by coherent morphisms of exact triangles $X_i\rightarrow Y_i\rightarrow Z_i\rightarrow \Sigma X_i$ in ${\mathcal {C}}$, we form in ${\mathcal {D}}$ its colimit and obtain an exact triangle (4.3); it does not depend on any choices. Conversely, fix an exact triangle $\eta :{\bar{X}}\rightarrow {\bar{Y}}\rightarrow {\bar{Z}}\rightarrow \Sigma {\bar{X}}$ in ${\mathcal {D}}$ that is given by $X,Y\in {\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$ with ${\bar{X}}=\mathop {\mathrm{colim }}\limits _i X_i$ and ${\bar{Y}}=\mathop {\mathrm{colim }}\limits _i Y_i$. The morphism ${\bar{X}}\rightarrow {\bar{Y}}$ is up to isomorphism given by a morphism $\phi :X\rightarrow Y$ in ${\text {Cauch }}({\mathbb {N}},{\mathcal {C}})$, so of the form $\mathop {\mathrm{colim }}\limits _i\phi _i$. Now complete the $\phi _i:X_i\rightarrow Y_i$ to a sequence of coherent morphisms between exact triangles $X_i\rightarrow Y_i\rightarrow Z_i\rightarrow \Sigma X_i$ in ${\mathcal {C}}$. It is easily checked that $(Z_i)_{i\ge 0}$ is a Cauchy sequence; set ${\tilde{Z}}:=\mathop {\mathrm{colim }}\limits _i Z_i$. This yields an exact triangle $\eta ':{\bar{X}}\rightarrow {\bar{Y}}\rightarrow \tilde{Z}\rightarrow \Sigma {\bar{X}}$ in ${\mathcal {T}}$, keeping in mind the above remark about homotopy colimits of exact triangles. It follows that ${\mathcal {D}}$ is closed under the formation of cones and therefore a triangulated subcategory of ${\mathcal {T}}$. Clearly, $\eta$ and $\eta '$ are isomorphic triangles. Thus any exact triangle in ${\mathcal {D}}$ is up to isomorphism a colimit of exact triangles in ${\mathcal {C}}$. $\square$

Corollary 4.8

Let ${\mathcal {T}}$ be an algebraic triangulated category with countable coproducts and ${\mathcal {C}}\subseteq {\mathcal {T}}$ a full triangulated subcategory consisting of compact objects. Suppose the class of Cauchy sequences in ${\mathcal {C}}$ is phantomless. Then the full subcategory

$$\begin{aligned} \{\mathop {\mathrm{hocolim }}\limits _i X_i\in {\mathcal {T}}\mid X\in {\text {Cauch }}({\mathbb {N}},{\mathcal {C}})\}\subseteq {\mathcal {T}}\end{aligned}$$

is a triangulated subcategory which is triangle equivalent to ${\widehat{{\mathcal {C}}}}$. The exact triangles are precisely the ones isomorphic to colimits of Cauchy sequences given by coherent morphisms of exact triangles in ${\mathcal {C}}$. $\square$

For a generalisation of Corollary 4.8 from algebraic triangulated categories to triangulated categories with a morphic enhancement, see Sect. C.7.

Remark 4.9

To be phantomless is a condition which can be checked for a specific sequence $Y=(Y_i)_{i\ge 0}$ in ${\mathcal {C}}$. Given $C\in {\mathcal {C}}$, call a subgroup

$$\begin{aligned} U\subseteq {\widetilde{Y}}(C)=\mathop {\mathrm{colim }}\limits _j{\text {Hom}}(C,Y_j) \end{aligned}$$

of finite definition if it arises as the image of a map ${\widetilde{Y}}(D)\rightarrow {\widetilde{Y}}(C)$ for some morphism $C\rightarrow D$ in ${\mathcal {C}}$; see [15]. The descending chain condition (dcc) for subgroups of finite definition implies that (4.2) holds for all sequences X in ${\mathcal {C}}$, since it implies the Mittag–Leffler condition for

$$\begin{aligned} \cdots \longrightarrow {\widetilde{Y}}(X_2)\longrightarrow {\widetilde{Y}}(X_1) \longrightarrow \widetilde{Y}(X_0). \end{aligned}$$

The dcc for subgroups of finite definition is equivalent to Y being $\Sigma$-pure-injective when viewed as an object in ${\text {Ind }}({\mathcal {C}})$, by [9, Sect. 3.5]. On the other hand, when ${\mathcal {T}}$ is a compactly generated triangulated category, then $Z\in {\mathcal {T}}$ is pure-injective if and only if ${\text {Ph }}(-,Z)=0$, by [22, Theorem 1.8].

Let ${\mathcal {C}}$ be a triangulated category and fix a cohomological functor $H:{\mathcal {C}}\rightarrow {\mathcal {A}}$ into an abelian category. Set $H^n:=H\circ \Sigma ^n$ for $n\in {\mathbb {Z}}$. We call a sequence $(X_i)_{i\ge 0}$ in ${\mathcal {C}}$ bounded if

$$\begin{aligned} \mathop {\mathrm{colim }}\limits _{i}H^{n}(X_i)=0\quad \text {for} \quad |n|\gg 0 \end{aligned}$$

and write

$$\begin{aligned} {{\widehat{{\mathcal {C}}}}}^b:=\{X\in {\widehat{{\mathcal {C}}}}\mid X \text { bounded}\} \end{aligned}$$

for the full subcategory of bounded objects.

Remark 4.10

Suppose for all $C\in {\mathcal {C}}$ that $H^n(C)=0$ for $|n|\gg 0$. Then we may restrict ourselves to bounded Cauchy sequences, and if this class is phantomless, then the conclusion of Theorem 4.7 holds for ${\widehat{{\mathcal {C}}}}^b$.

More generally, fix a class ${\mathcal {X}}\subseteq {\text {Fun}}({\mathbb {N}},{\mathcal {C}})$ that is closed under suspensions and cones. When ${\mathcal {X}}$ is phantomless, then the conclusion of Corollary 4.8 holds for

$$\begin{aligned} \widehat{{\mathcal {C}}_{\mathcal {X}}}\xrightarrow {\ _\sim \ }\{\mathop {\mathrm{hocolim }}\limits _i X_i\in {\mathcal {T}}\mid X\in {\mathcal {X}}\}. \end{aligned}$$

For more details, cf. Sect. C.5.

Example 4.11

Let $\Lambda$ be a quasi-Frobenius ring of finite representation type. Then the class of all sequences in the stable category ${\text {St }}({\text {mod }}\Lambda )$ is phantomless. In fact, this holds for any locally finite triangulated category [24, 41] and can be deduced from Remark 4.9.

The following example is a continuation of our discussion in Sect. 3. For an abelian category ${\mathcal {A}}$ let ${\mathbf {D}}^b({\mathcal {A}})$ denote its bounded derived category. An object in ${\mathcal {A}}$ is locally finite if it is a directed union of finite length subobjects.

Example 4.12

Let k be a commutative ring and ${\mathcal {A}}$ a k-linear Grothendieck category such that ${\text {Hom}}(X,Y)$ is a finite length k-module for all $X,Y\in {\text {fl }}{\mathcal {A}}$. Suppose that there are only finitely many isomorphism classes of simple objects and that the injective envelope of each simple object is locally finite and artinian. Then the class of Cauchy sequences in ${\mathbf {D}}^b({\text {fl }}{\mathcal {A}})$ is phantomless and we have triangle equivalences

$$\begin{aligned} {\mathbf {D}}^b(\widehat{{\text {fl }}{\mathcal {A}}}) \xrightarrow {\ _\sim \ }{\mathbf {D}}^b({\text {art }}{\mathcal {A}})\xrightarrow {\ _\sim \ }\widehat{{\mathbf {D}}^b({\text {fl }}{\mathcal {A}})}^b. \end{aligned}$$

Proof

The first equivalence is clear from Proposition 3.4; so we focus on the second one. We may assume that all objects in ${\mathcal {A}}$ are locally finite. For all $X,Y\in {\mathbf {D}}^b({\text {fl }}{\mathcal {A}})$ the k-module ${\text {Hom}}(X,Y)$ has finite length, since ${\text {Ext }}^n(S,T)$ has finite length for all simple S, T and $n \ge 0$ by our assumptions on ${\mathcal {A}}$. It follows that the class of Cauchy sequences in ${\mathbf {D}}^b({\text {fl }}{\mathcal {A}})$ is phantomless by the Mittag–Leffler condition. We wish to apply Corollary 4.8 and choose for ${\mathcal {T}}$ the category ${\mathbf {K}}({\text {Inj }}{\mathcal {A}})$ of complexes up to homotopy, where ${\text {Inj }}{\mathcal {A}}$ denotes the full subcategory of injective objects in ${\mathcal {A}}$. Set ${\text {inj }}{\mathcal {A}}={\text {Inj }}{\mathcal {A}}\cap {\text {art }}{\mathcal {A}}$. Then ${\mathbf {D}}^b({\text {fl }}{\mathcal {A}})$ identifies with ${\mathcal {T}}^c$ via

$$\begin{aligned} F:{\mathbf {D}}^b({\text {art }}{\mathcal {A}})\xrightarrow {_\sim }{\mathbf {K}}^{+,b}({\text {inj }}{\mathcal {A}}) \hookrightarrow {\mathbf {K}}({\text {Inj }}{\mathcal {A}}), \end{aligned}$$

by [23, Proposition 2.3]. Set ${\mathcal {C}}:={\mathbf {D}}^b({\text {fl }}{\mathcal {A}})$. Then Corollary 4.8 yields a triangle equivalence

$$\begin{aligned} {\widehat{{\mathcal {C}}}}\xrightarrow {\ _\sim \ }{\mathcal {D}}:=\{\mathop {\mathrm{hocolim }}\limits _i X_i\in {\mathcal {T}}\mid X\in {\text {Cauch }}({\mathbb {N}},{\mathcal {C}})\}. \end{aligned}$$

We claim that F induces an equivalence

$$\begin{aligned} {\mathbf {D}}^b({\text {art }}{\mathcal {A}})\xrightarrow {_\sim }{\mathcal {D}}^b:=\{X\in {\mathcal {D}}\mid \mathop {\mathrm{colim }}\limits _iH^n(X_i)=0\text { for } |n|\gg 0\}. \end{aligned}$$

Any object $M\in {\text {art }}{\mathcal {A}}$ is the colimit of the Cauchy sequence $({\text {soc }}^iM)_{i\ge 0}$ in ${\text {fl }}{\mathcal {A}}$ by Proposition 3.4, and this yields a Cauchy sequence in ${\mathbf {D}}^b({\text {fl }}{\mathcal {A}})$. Thus F maps ${\text {art }}{\mathcal {A}}$ into ${\mathcal {D}}^b$, and therefore also ${\mathbf {D}}^b({\text {art }}{\mathcal {A}})$, since F is an exact functor and ${\mathbf {D}}^b({\text {art }}{\mathcal {A}})$ is generated by ${\text {art }}{\mathcal {A}}$ as a triangulated category. Conversely, let ${\bar{X}}=\mathop {\mathrm{colim }}\limits \nolimits _i X_i$ be an object in ${\mathcal {D}}^b$. We may assume that the complex ${\bar{X}}$ is homotopically minimal, as in [23, Appendix B]. The Cauchy condition implies for each simple $S\in {\mathcal {A}}$ and $n\in {\mathbb {Z}}$ that ${\text {Hom}}(S,\Sigma ^n {\bar{X}})$ has finite length over k, so the degree n component of ${\bar{X}}$ is artinian. Thus ${\bar{X}}$ belongs to ${\mathbf {K}}^{+,b}({\text {inj }}{\mathcal {A}})$, and this yields the claim. $\square$

5 Homologically perfect objects

Let ${\mathcal {T}}$ be a compactly generated triangulated category and denote by ${\mathcal {T}}^c$ the full subcategory of compact objects. We fix a cohomological functor $H:{\mathcal {T}}\rightarrow {\mathcal {A}}$ into an abelian category. For $n\in {\mathbb {Z}}$ set $H^n:=H\circ \Sigma ^n$.

Definition 5.1

We say that an object X in ${\mathcal {T}}$ is homologically perfect (with respect to H) if X can be written as homotopy colimit of a sequence $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {T}}^c$ such that the following holds:

• (HP1) The sequence $(X_i)_{i\ge 0}$ is a Cauchy sequence in ${\mathcal {T}}^c$, that is, for every $C\in {\mathcal {T}}^c$

  $$\begin{aligned} {\text {Hom}}(C,X_i)\xrightarrow {_\sim }{\text {Hom}}(C,X_{i+1})\quad \text {for}\quad i\gg 0. \end{aligned}$$

• (HP2) For every $n\in {\mathbb {Z}}$ we have $H^n(X_i)\xrightarrow {_\sim }H^n(X_{i+1})$ for $i\gg 0$.

• (HP3) For almost all $n\in {\mathbb {Z}}$ we have $H^n(X_i)=0$ for $i\gg 0$.

When ${\mathcal {T}}$ is the derived category of an abelian category, then our choice of H is the natural one given by the degree zero cohomology of a complex, unless stated otherwise.

It is clear that the above definition depends on the choice of H; so a different choice of H may yield a different class of homologically perfect objects. However, in our applications there are natural choices for H, for instance when ${\mathcal {T}}$ is the derived category of an abelian category. It is a remarkable fact that in those cases there is an intrinsic description of homologically perfect objects that depends only on ${\mathcal {T}}$. That means some choices of H are more natural than others. The following Lemma 5.3 makes this precise when the cohomological functor H is given by a compact generator. For noetherian schemes that are non-affine, the natural choice for H admits the same intrinsic description of homologically perfect objects, but the proof is more involved and we refer to Theorem B.1.

We begin with an elementary but useful observation.

Lemma 5.2

Let ${\mathcal {C}}$ be a triangulated category and $G\in {\mathcal {C}}$ an object that generates ${\mathcal {C}}$, that is, ${\mathcal {C}}$ admits no proper thick subcategory containing G. Then a sequence $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {C}}$ is Cauchy if and only if for all $n\in {\mathbb {Z}}$ we have ${\text {Hom}}(\Sigma ^n G,X_i)\xrightarrow {_\sim }{\text {Hom}}(\Sigma ^n G,X_{i+1})$ for $i\gg 0$. $\square$

The following yields an intrinsic description of homologically perfect objects.

Lemma 5.3

Let G be a compact object in ${\mathcal {T}}$ that generates ${\mathcal {T}}^c$ as a triangulated category. Then for $X\in {\mathcal {T}}$ the following are equivalent:

• (1) The object X is homologically perfect with respect to $H={\text {Hom}}(G,-)$.

• (2) The object X can be written as homotopy colimit of a Cauchy sequence in ${\mathcal {T}}^c$, and for every $C\in {\mathcal {T}}^c$ we have ${\text {Hom}}(C,\Sigma ^nX)=0$ for $|n|\gg 0$.

Proof

The assumption on H implies that the conditions (HP1) and (HP2) are equivalent, thanks to Lemma 5.2. Condition (HP3) means $H^n(X)=0$ for $|n|\gg 0$, since $H^n(X)\cong \mathrm{colim}_{i} H^n(X_i)$ by Lemma 4.1. Thus (HP3) is equivalent to the condition that for every $C\in {\mathcal {T}}^c$ we have ${\text {Hom}}(C,\Sigma ^nX)=0$ for $|n|\gg 0$, since G generates ${\mathcal {T}}^c$. $\square$

Now fix a ring $\Lambda$. We write ${\mathbf {D}}(\Lambda )$ for the derived category of the abelian category of all $\Lambda$-modules. Let ${\mathbf {D}}^\mathrm {per}(\Lambda )$ denote the full subcategory of perfect complexes, that is, objects isomorphic to bounded complexes of finitely generated projective modules. The triangulated category ${\mathbf {D}}(\Lambda )$ is compactly generated and the compact objects are precisely the perfect complexes.

Let ${\text {mod }}\Lambda$ denote the category of finitely presented $\Lambda$-modules and ${\text {proj }}\Lambda$ denotes the full subcategory of finitely generated projective modules. When $\Lambda$ is a right coherent ring, then ${\text {mod }}\Lambda$ is abelian and we consider its derived category ${\mathbf {D}}^b({\text {mod }}\Lambda )$ using the following identifications

where the top row consists of categories of complexes of modules in ${\text {proj }}\Lambda$ up to homotopy. Note that ${\mathbf {D}}^\mathrm {per}(\Lambda )={\mathbf {D}}^b({\text {mod }}\Lambda )$ if and only if every finitely presented $\Lambda$-module has finite projective dimension.

We provide an intrinsic description of the objects from ${\mathbf {D}}^b({\text {mod }}\Lambda )$, which uses for any complex X the sequence of truncations

$$\begin{aligned} \cdots \longrightarrow \sigma _{\ge n+1}X\longrightarrow \sigma _{\ge n}X\longrightarrow \sigma _{\ge n-1}X\longrightarrow \cdots \end{aligned}$$

given by

In the following lemma we use the notion of a homologically perfect object with respect to the functor that takes degree zero cohomology of a complex, keeping in mind Lemma 5.3.

Lemma 5.4

Let $\Lambda$ be a right coherent ring. Then X in ${\mathbf {D}}(\Lambda )$ is homologically perfect if and only if X belongs to ${\mathbf {D}}^b({\text {mod }}\Lambda )$.

Proof

Let X be a complex in ${\mathbf {K}}^{-,b}({\text {proj }}\Lambda )={\mathbf {D}}^b({\text {mod }}\Lambda )$ and write X as homotopy colimit of its truncations $X_i=\sigma _{\ge -i}X$ which lie in ${\mathbf {K}}^{b}({\text {proj }}\Lambda )$. It is clear that X is homologically perfect. In fact, ${\mathbf {D}}^\mathrm {per}(\Lambda )$ is generated by $\Lambda$; so it suffices to check the functor $H^n={\text {Hom}}(\Lambda ,\Sigma ^{n}-)$ for every $n\in {\mathbb {Z}}$. We have $H^n(X_i)\xrightarrow {_\sim }H^n(X_{i+1})$ for $i\gg 0$ and $H^nX=0$ for $|n|\gg 0$. On the other hand, if X is homologically perfect, then $H^nX$ is finitely presented for all n, so X lies in ${\mathbf {D}}^b({\text {mod }}\Lambda )$. $\square$

6 The bounded derived category

Let $\Lambda$ be a ring. We consider the category ${\text {mod }}\Lambda$ of finitely presented $\Lambda$-modules and its bounded derived category ${\mathbf {D}}^b({\text {mod }}\Lambda )$. Our aim is to identify ${\mathbf {D}}^b({\text {mod }}\Lambda )$ with a completion of ${\mathbf {D}}^\mathrm {per}(\Lambda )$ when $\Lambda$ is right coherent; compare this with Rouquier’s [38, Corollary 6.4].

Lemma 6.1

Let $\Lambda$ be a ring and set ${\mathcal {P}}={\text {proj }}\Lambda$. Then the functor

$$\begin{aligned} {\mathbf {K}}^{-,b}({\mathcal {P}})\longrightarrow {\text {Add }}({\mathbf {K}}^b({\mathcal {P}})^\mathrm {op},\mathrm {Ab}),\quad X\mapsto h_X:={\text {Hom}}(-,X)|_{{\mathbf {K}}^b({\mathcal {P}})}, \end{aligned}$$

is fully faithful.

Proof

We view ${\mathbf {K}}^{-,b}({\mathcal {P}})$ as a subcategory of ${\mathbf {D}}(\Lambda )$. Let X, Y be objects in ${\mathbf {K}}^{-,b}({\mathcal {P}})$ and write X as homotopy colimit of its truncations $X_i=\sigma _{\ge -i}X$ which lie in ${\mathbf {K}}^{b}({\mathcal {P}})$. Let $C_i$ denote the cone of $X_{i}\rightarrow X_{i+1}$. This complex is concentrated in degree $-i-1$; so ${\text {Hom}}(C_i,Y)=0$ for $i\gg 0$. Thus $X_{i}\rightarrow X_{i+1}$ induces a bijection

$$\begin{aligned} {\text {Hom}}(X_{i+1},Y)\xrightarrow {_\sim }{\text {Hom}}(X_{i},Y) \quad \text {for}\quad i\gg 0. \end{aligned}$$

This implies

$$\begin{aligned} {\text {Hom}}(X,Y)\xrightarrow {_\sim }\lim _i{\text {Hom}}(X_i,Y) \end{aligned}$$

and therefore ${\text {Ph }}(X,Y)=0$ by Lemma 4.2. From Lemma 4.3 we conclude that

$$\begin{aligned} {\text {Hom}}(X,Y)\xrightarrow {_\sim }{\text {Hom}}(h_X,h_Y). \end{aligned}$$

$\square$

Let ${\mathcal {C}}$ be a triangulated category and fix a cohomological functor $H:{\mathcal {C}}\rightarrow {\mathcal {A}}$. Recall that an object X in ${\widehat{{\mathcal {C}}}}$ is bounded if $\mathop {\mathrm{colim }}\limits \nolimits _iH^n(X_i)=0$ for $|n|\gg 0$, and ${\widehat{{\mathcal {C}}}}^b$ denotes the full subcategory of bounded objects in ${\widehat{{\mathcal {C}}}}$. From Theorem 4.7 and Remark 4.10 we know that ${\widehat{{\mathcal {C}}}}^b$ admits a canonical triangulated structure when ${\mathcal {C}}$ is algebraic and bounded Cauchy sequences are phantomless.

Theorem 6.2

For a right coherent ring $\Lambda$ there is a canonical triangle equivalence

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}(\Lambda )}^b\xrightarrow {\ _\sim \ }{\mathbf {D}}^b({\text {mod }}\Lambda ) \end{aligned}$$

which sends a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}(\Lambda )$ to its colimit.

Proof

We consider the functor

$$\begin{aligned} {\mathbf {D}}^b({\text {mod }}\Lambda )\longrightarrow {\text {Add }}({\mathbf {D}}^\mathrm {per}(\Lambda )^\mathrm {op},\mathrm {Ab}),\quad X\mapsto {\text {Hom}}(-,X)|_{{\mathbf {D}}^\mathrm {per}(\Lambda )}, \end{aligned}$$

which is fully faithful by Lemma 6.1. On the other hand, we have the functor

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}(\Lambda )}^b\longrightarrow {\text {Add }}({\mathbf {D}}^\mathrm {per}(\Lambda )^\mathrm {op},\mathrm {Ab}), \quad X\mapsto {\widetilde{X}}, \end{aligned}$$

which is fully faithful by Proposition 2.4. Both functors have the same essential image by Lemma 5.4, because we can identify this with a full subcategory of ${\mathbf {D}}(\Lambda )$ by Lemma 4.6. This yields a triangle equivalence, since the triangulated structures of both categories identify with the one from ${\mathbf {D}}(\Lambda )$; see Corollary 4.8 plus Remark 4.10. $\square$

Remark 6.3

The triangulated category ${\mathbf {D}}^\mathrm {per}(\Lambda )$ admits a morphic enhancement which is given by ${\mathbf {D}}^\mathrm {per}(\Lambda _1)$, with $\Lambda _1$ the ring of upper triangular $2\times 2$ matrices over $\Lambda$. This enhancement can be completed and yields a morphic enhancement of $\widehat{{\mathbf {D}}^\mathrm {per}(\Lambda )}^b$ that identifies with the morphic enhancement of ${\mathbf {D}}^b({\text {mod }}\Lambda )$; see Sect. C.8. This observation enriches the triangle equivalence of Theorem 6.2.

For a noetherian algebra over a complete local ring, there is another description of ${\mathbf {D}}^b({\text {mod }}\Lambda )$ which is obtained by completing the category of finite length modules over $\Lambda ^\mathrm {op}$.

Proposition 6.4

Let $\Lambda$ be a noetherian algebra over a complete local ring and set $\Gamma =\Lambda ^\mathrm {op}$. Then there are triangle equivalences

$$\begin{aligned} {\mathbf {D}}^b({\text {mod }}\Lambda )^\mathrm {op}\xrightarrow {\ _\sim \ }{\mathbf {D}}^b(\widehat{{\text {fl }}\Gamma }) \xrightarrow {\ _\sim \ }\widehat{{\mathbf {D}}^b({\text {fl }}\Gamma )}^b. \end{aligned}$$

Proof

Matlis duality gives an equivalence $({\text {mod }}\Lambda )^\mathrm {op}\xrightarrow {_\sim }{\text {art }}\Gamma$, so ${\mathbf {D}}^b({\text {mod }}\Lambda )^\mathrm {op}\xrightarrow {_\sim }{\mathbf {D}}^b({\text {art }}\Gamma )$, and we have ${\text {art }}\Gamma \xrightarrow {_\sim }\widehat{{\text {fl }}\Gamma }$ by Example 3.6. This yields the first functor, and the second is from Example 4.12. $\square$

7 Pseudo-coherent objects

Let ${\mathcal {T}}$ be a triangulated category and $H:{\mathcal {T}}\rightarrow {\mathcal {A}}$ a cohomological functor into an abelian category. Set

$$\begin{aligned} {\mathcal {T}}^{> n}:=\{X\in {\mathcal {T}}\mid H^iX=0\text { for all }i \le n\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {T}}^{\le n}:=\{X\in {\mathcal {T}}\mid H^iX=0\text { for all }i > n\}. \end{aligned}$$

We suppose for all $X,Y\in {\mathcal {T}}$ and $n\in {\mathbb {Z}}$ the following:

• (TS1) There is an exact triangle

  $$\begin{aligned} \tau _{\le n}X\longrightarrow X\longrightarrow \tau _{>n}X \longrightarrow \Sigma (\tau _{\le n}X) \end{aligned}$$

  with $\tau _{\le n}X\in {\mathcal {T}}^{\le n}$ and $\tau _{> n}X\in {\mathcal {T}}^{> n}$.

• (TS2) ${\text {Hom}}(X,Y)=0$ for $X\in {\mathcal {T}}^{\le n}$ and $Y\in {\mathcal {T}}^{>n}$.

Thus the category ${\mathcal {T}}$ is equiped with a t-structure [1].

We will use the following observation.

Lemma 7.1

For any morphism $X\rightarrow Y$ in ${\mathcal {T}}$ we have

$$\begin{aligned} \tau _{>n}X\xrightarrow {_\sim }\tau _{>n}Y\iff H^iX\xrightarrow {_\sim }H^iY\text { for all } i>n. \end{aligned}$$

Proof

Note that for any object X the morphism $X\rightarrow \tau _{>n}X$ induces an isomorphism $H^iX\rightarrow H^i(\tau _{>n}X)$ for all $i>n$. Thus $H^iX\xrightarrow {_\sim }H^iY$ for all $i>n$ if and only if $H^i(\tau _{>n}X)\xrightarrow {_\sim }H^i(\tau _{>n}Y)$ for all $i\in {\mathbb {Z}}$. $\square$

Now suppose that ${\mathcal {T}}$ is compactly generated and write ${\mathcal {T}}^c$ for the full subcategory of compact objects.

Definition 7.2

An object $X\in {\mathcal {T}}$ is called pseudo-coherent (with respect to the chosen t-structure) if X can be written as homotopy colimit of a sequence $X_0\rightarrow X_1\rightarrow X_2\rightarrow \cdots$ in ${\mathcal {T}}^c$ such that $\tau _{>-i} X_i\xrightarrow {_\sim } \tau _{> -i} X$ for all $i\ge 0$. We say that X has bounded cohomology if $H^nX=0$ for $|n|\gg 0$.

Lemma 7.3

The functor

$$\begin{aligned} {\mathcal {T}}\longrightarrow {\text {Add }}(({\mathcal {T}}^c)^\mathrm {op},\mathrm {Ab}),\quad X\mapsto h_X:={\text {Hom}}(-,X)|_{{\mathcal {T}}^c}, \end{aligned}$$

is fully faithful when restricted to pseudo-coherent objects with bounded cohomology.

Proof

Let X, Y be objects in ${\mathcal {T}}$. Suppose that $X= \mathop {\mathrm{hocolim }}\limits _iX_i$ is pseudo-coherent and $H^nY=0$ for $n\ll 0$. Let $C_i$ denote the cone of $X_{i}\rightarrow X_{i+1}$. The induced morphism $\tau _{> -i}X_i\rightarrow \tau _{>-i}X_{i+1}$ is an isomorphism since $\tau _{>-i}\tau _{>-(i+1)}=\tau _{>-i}$. Thus $C_i\in {\mathcal {T}}^{\le -i}$ and therefore ${\text {Hom}}(X_{i+1},Y)\xrightarrow {_\sim }{\text {Hom}}(X_{i},Y)$ for $i\gg 0$. It follows from Lemma 4.2 that ${\text {Ph }}(X,Y)=0$, so

$$\begin{aligned} {\text {Hom}}(X,Y)\xrightarrow {_\sim }{\text {Hom}}(h_X,h_Y) \end{aligned}$$

by Lemma 4.3. $\square$

Example 7.4

Let $\Lambda$ be a ring and ${\mathcal {T}}={\mathbf {D}}(\Lambda )$ the derived category of the category of all $\Lambda$-modules with the standard t-structure. Then the canonical functor ${\mathbf {K}}^-({\text {proj }}\Lambda )\rightarrow {\mathbf {D}}(\Lambda )$ identifies ${\mathbf {K}}^-({\text {proj }}\Lambda )$ with the full subcategory of pseudo-coherent objects in ${\mathbf {D}}(\Lambda )$.

Proof

For $X\in {\mathbf {K}}^-({\text {proj }}\Lambda )$ and $i\ge 0$ set $X_i:=\sigma _{\ge -i}X$. Then we have $X={\mathrm{hocolim}_{i}} X_i=X$ and $\tau _{>-i} X_i\xrightarrow {_\sim } \tau _{> -i} X$ for all $i\ge 0$. Thus X is pseudo-coherent. The other implication is left to the reader. $\square$

The example shows that for a right coherent ring $\Lambda$ and any object X in ${\mathcal {T}}={\mathbf {D}}(\Lambda )$ the following are equivalent:

• (PC) X is pseudo-coherent and has bounded cohomology.

• (HP) X is homologically perfect.

This seems to be a common phenomenon (cf. Propositions 8.1 and A.1) though we do not have a general proof.

Let ${\mathcal {C}}$ be a triangulated category and fix a cohomological functor $H:{\mathcal {C}}\rightarrow {\mathcal {A}}$. Call a sequence $(X_i)_{i\ge 0}$ in ${\mathcal {C}}$ strongly bounded if ${\mathrm{colim}}_{i} H^n(X_i)=0$ for $|n|\gg 0$, and if for every $n\in {\mathbb {Z}}$ we have $H^n(X_i)\xrightarrow {_\sim }H^n(X_{i+1})$ for $i\gg 0$. By abuse of notation, we write ${\widehat{{\mathcal {C}}}}^b$ for the full subcategory of strongly bounded objects in ${\widehat{{\mathcal {C}}}}$.²

Lemma 7.5

Suppose that (PC) $\Leftrightarrow$ (HP) for all $X\in {\mathcal {T}}$, and set ${\mathcal {C}}:={\mathcal {T}}^c$. Then the functor

$$\begin{aligned} F:\widehat{{\mathcal {C}}}^b\longrightarrow {\mathcal {T}},\quad X\mapsto \mathop {\mathrm{hocolim }}\limits _i X_i, \end{aligned}$$

is fully faithful functor and identifies $\widehat{{\mathcal {C}}}^b$ with the full subcategory of pseudo-coherent objects having bounded cohomology. When ${\mathcal {T}}$ admits a morphic enhancement, then F is a triangle functor.

Proof

The first assertion follows from Lemmas 4.6 and 7.3. For the second assertion, see Lemma C.10. $\square$

8 Noetherian schemes

We fix a noetherian scheme ${\mathbb {X}}$. Let ${\text {Qcoh }}{\mathbb {X}}$ denote the category of quasi-coherent sheaves on ${\mathbb {X}}$, and ${\text {coh }}{\mathbb {X}}$ denotes the full subcategory of coherent sheaves. We consider the derived categories

$$\begin{aligned} {\mathbf {D}}^\mathrm {per}({\mathbb {X}})\hookrightarrow {\mathbf {D}}^b({\text {coh }}{\mathbb {X}})\hookrightarrow {\mathbf {D}}({\text {Qcoh }}{\mathbb {X}}). \end{aligned}$$

The triangulated category ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ is compactly generated and the full subcategory of compact objects agrees with the category ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$ of perfect complexes [31]. We use the standard t-structure and then the above notion of a pseudo-coherent object identifies with the usual one; see [17, Sect. 2.3], [40, Sect. 2.2], and [39, §0DJM]. A precise reference is [39, Lemma 0DJN], which uses approximations and builds on work of Lipman and Neeman [25].

We obtain the following description of the objects in ${\mathbf {D}}^b({\text {coh }}{\mathbb {X}})$. For a refinement, see Theorem B.1. We use the notion of a homologically perfect object with respect to the functor that takes degree zero cohomology of a complex.

Proposition 8.1

For an object X in ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ the following are equivalent:

• (1) X belongs to ${\mathbf {D}}^b({\text {coh }}{\mathbb {X}})$.

• (2) X is pseudo-coherent and has bounded cohomology.

• (3) X is homologically perfect.

Proof

(1) $\Leftrightarrow$ (2): See [40, Example 2.2.8].

(2) $\Rightarrow$ (3): Let $X={\mathrm{hocolim}}_{i} X_i$ be pseudo-coherent and C a perfect complex. The argument in the proof of Lemma 7.3 shows that $(X_i)_{i\ge 0}$ is a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$. More precisely, the cone of $X_{i}\rightarrow X_{i+1}$ belongs to ${\mathcal {T}}^{\le -i}$, and therefore ${\text {Hom}}(C,X_i)\xrightarrow {_\sim }{\text {Hom}}(C,X_{i+1})$ for $i\gg 0$; see [39, §09M2]. Also, $H^n(X_i)\xrightarrow {_\sim }H^n(X_{i+1})$ for all $i>-n$. Finally, for almost all $n\in {\mathbb {Z}}$ we have $H^n(X_i)\cong H^n(X)=0$ for $i\gg 0$, since X has bounded cohomology.

(3) $\Rightarrow$ (1): Let $X={\mathrm{hocolim}}_{i} X_i$ be homologically perfect and $n\in {\mathbb {Z}}$. Then $H^n(X)\cong \mathop {\mathrm{colim }}\limits _i H^n(X_i)$ equals the cohomology of some perfect complex, so $H^n(X)$ is coherent. Also, $H^n(X)=0$ for $|n|\gg 0$. $\square$

The following is now the analogue of Theorem 6.2 for schemes that are not necessarily affine. The proof is very similar; see also Lemma 7.5 for the general argument.

Theorem 8.2

For a noetherian scheme ${\mathbb {X}}$ there is a canonical triangle equivalence

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}^b\xrightarrow {\ _\sim \ }{\mathbf {D}}^b({\text {coh }}{\mathbb {X}}) \end{aligned}$$

which sends a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$ to its colimit.

Proof

We consider the functor

$$\begin{aligned} {\mathbf {D}}^b({\text {coh }}{\mathbb {X}})\longrightarrow {\text {Add }}({\mathbf {D}}^\mathrm {per}({\mathbb {X}})^\mathrm {op},\mathrm {Ab}),\quad X\mapsto {\text {Hom}}(-,X)|_{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}, \end{aligned}$$

which is fully faithful by Lemma 7.3 and Proposition 8.1. On the other hand, we have the functor

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}^b\longrightarrow {\text {Add }}({\mathbf {D}}^\mathrm {per}({\mathbb {X}})^\mathrm {op},\mathrm {Ab}), \quad X\mapsto {\widetilde{X}}, \end{aligned}$$

which is fully faithful by Proposition 2.4. Both functors have the same essential image by Proposition 8.1, because we can identify this with a full subcategory of ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ by Lemma 4.6. This yields a triangle equivalence, since the triangulated structures of both categories identify with the one from ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$; see Corollary 4.8 plus Remark 4.10. $\square$

An immediate consequence is the following.

Corollary 8.3

The singularity category of ${\mathbb {X}}$ (in the sense of Buchweitz and Orlov [4, 37]) identifies with the Verdier quotient

$$\begin{aligned} \frac{\widehat{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}^b}{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}. \end{aligned}$$

$\square$

Appendices

Appendix A: homologically perfect objects in homotopy theory

by Tobias Barthel

Let R be an associative ring spectrum and let ${\mathcal {D}}_R$ be the derived category of right R-module spectra as constructed for example in [10]; if no confusion is likely to arise, we will refer to an object in ${\mathcal {D}}_R$ simply as an R-module. If R is connective, then ${\mathcal {D}}_R$ inherits the standard t-structure from the stable homotopy category, and we denote by ${\mathcal {D}}_R^b\subseteq {\mathcal {D}}_R$ the full triangulated subcategory of bounded R-module spectra, i.e., those R-modules M with $\pi _iM$ finitely presented over $\pi _0R$ and $\pi _iM = 0$ for $|i |\gg 0$. As usual, ${\mathcal {D}}_R^c \subseteq {\mathcal {D}}_R$ is the full subcategory of compact R-modules or, equivalently, the thick subcategory generated by the right R-module R.

Throughout this appendix, we will employ homological grading, so for example the pseudo-coherence condition $\tau _{>-i}M_i \xrightarrow {_\sim } \tau _{>-i}M$ introduced in Sect. 7 translates to $\pi _jM_i \xrightarrow {_\sim } \pi _jM$ for all $j <i$. Furthermore, the notion of homologically perfect object used here will always be with respect to the homological functor $\pi _0$.

Proposition A.1

Suppose R is a connective associative ring spectrum with $\pi _0R$ right coherent and $\pi _iR$ finitely presented over $\pi _0R$ for all $i \ge 0$. The following conditions on $M \in {\mathcal {D}}_R$ are equivalent:

• (1) M is pseudo-coherent and has bounded homotopy.

• (2) M is homologically perfect.

• (3) M belongs to ${\mathcal {D}}_R^b$.

Proof

The implication (1) $\Rightarrow$ (2) is proven as in Proposition 8.1[(2) $\Rightarrow$ (3)]: indeed, it suffices to test against compact objects of the form $C = \Sigma ^nR$ for all $n\in {\mathbb {Z}}$, for which the claim is clear. In order to see that (2) $\Rightarrow$ (3), we first observe that any compact R-module has finitely presented homotopy groups by assumption on R. Therefore, any homologically perfect $M \in {\mathcal {D}}_R$ can only have finitely many nonzero homotopy groups, all of which must be finitely presented over $\pi _0R$ by the Cauchy condition. Thus, M is bounded.

Now assume that $M \in {\mathcal {D}}_R^b$, then M has bounded homotopy and it remains to show that M has to be pseudo-coherent. To this end, we use a mild variant of the cellular tower construction of [10, Thm. III.2.10] or [16, Prop. 2.3.1], in which we only attach R-cells of a fixed dimension in each step. Indeed, let $M \in {\mathcal {D}}_R$ be a bounded below R-module with finitely presented homotopy groups and assume without loss of generality that the lowest nonzero homotopy group is in degree 0. Inductively, we construct a tower of R-modules $(M^k)_{k \ge 0}$ under M with:

• (i) $M^0 = M$.

• (ii) For all $k\ge 0$, there is a cofiber sequence

  $$\begin{aligned} F^k=\bigoplus _{G(k)} \Sigma ^kR \longrightarrow M^k \longrightarrow M^{k+1}, \end{aligned}$$

  where the direct sum is indexed by a set G(k) of generators of the finitely presented $\pi _0R$-module $\pi _kM^k$.

It follows by induction on k, the assumption on R, and the long exact sequence in homotopy that $\pi _*M^{k+1}$ is finitely presented over $\pi _0R$ in all degrees and zero below degree $k+1$, which allows us to construct the map $F^{k+1} \rightarrow M^{k+1}$ and to proceed with the induction.

Set $M_k={{\,\mathrm{fib}\,}}(M \rightarrow M^k)$. The octahedral axiom provides fiber sequences

$$\begin{aligned} M_k \longrightarrow M_{k+1} \longrightarrow F^k \end{aligned}$$

(A.1)

and a sequence of R-modules

$$\begin{aligned} M_0 \longrightarrow M_1 \longrightarrow M_2 \longrightarrow \ldots \end{aligned}$$

over M. The fiber sequences (A.1) imply that $\pi _iM_k \xrightarrow {_\sim } \pi _iM_{k+1}$ and hence $\pi _iM_k \xrightarrow {_\sim } \pi _iM$ for all $i<k$, which then also shows that the homotopy colimit over $(M_k)_{k\ge 0}$ is equivalent to M by a connectivity argument. Moreover, because $M_k$ is built from finitely many R-cells, $M_k$ is compact for any $k\ge 0$. It follows that M is pseudo-coherent as desired. $\square$

In light of Lemma 7.5, we obtain the following consequence.

Corollary A.2

With notation as in Proposition A.1, taking homotopy colimits induces an equivalence $\widehat{{\mathcal {D}}_R^c}^b \xrightarrow {_\sim } {\mathcal {D}}_R^b$ of triangulated categories. $\square$

In particular, the corollary applied to the Eilenberg–Mac Lane ring spectrum $H\Lambda$ of a right coherent ring $\Lambda$ recovers Theorem 6.2.

Lemma A.3

Let R be as in Proposition A.1 and assume additionally that the right global dimension of $\pi _0R$ is finite, then ${\mathcal {D}}_R^b$ coincides with the thick subcategory of ${\mathcal {D}}_R^b$ generated by the Eilenberg–Mac Lane R-module $H\pi _0R$.

Proof

Since $\pi _0R$ has finite right global dimension, any finitely presented $\pi _0R$-module N admits a finite length resolution by finitely presented projective $\pi _0R$-modules. This implies that the R-module spectrum HN belongs to ${\text {Thick }}(H\pi _0R)$. A Postnikov tower argument then shows that any $M \in {\mathcal {D}}_R^b$ is in ${\text {Thick }}(H\pi _0R)$.

Conversely, since the R-module $H\pi _0R$ is bounded, so is any R-module that belongs to ${\text {Thick }}(H\pi _0R)$. $\square$

The stable homotopy category identifies with ${\mathcal {D}}_R$ for the sphere spectrum $R = S^0$ and we obtain the following consequence, a variant of which has appeared independently in work of Neeman [36, Ex. 22].

Corollary A.4

For a spectrum X in the stable homotopy category the following conditions are equivalent:

• (1) X is pseudo-coherent and has bounded homotopy.

• (2) X is homologically perfect.

• (3) X belongs to the thick subcategory generated by the spectrum $H{\mathbb {Z}}$.

In particular, a homologically perfect spectrum X is compact if and only if $X = 0$.

Proof

By the finite generation of the stable homotopy groups of spheres and because $\pi _0S^0 \cong {\mathbb {Z}}$, the sphere spectrum $R = S^0$ satisfies the conditions of the previous lemma, so we have ${\mathcal {D}}_{S^0}^b={\text {Thick }}(H{\mathbb {Z}})$.

A theorem of Serre says that a finite spectrum must have infinitely many nonzero homotopy groups, so this result implies in particular that a homologically perfect spectrum X is compact if and only if $X = 0$. $\square$

Note that, in contrast to the perfect derived categories of right coherent rings or noetherian schemes, the category ${\mathcal {D}}_{S^0}^b$ does not contain ${\mathcal {D}}_{S^0}^c$ as a subcategory.

Appendix B: homologically perfect objects on noetherian schemes

by Tobias Barthel and Henning Krause

Throughout this appendix, all schemes will be assumed to be separated and noetherian. For a scheme ${\mathbb {X}}$, we write ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ for the derived category of quasi-coherent sheaves on ${\mathbb {X}}$ and $G_{\mathbb {X}}$ denotes a compact generator of ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$, which exists by [3, Thm. 3.3.1]. The notion of homologically perfect object considered in this appendix is defined with respect to the cohomological functor $H^0$, taking the degree zero cohomology of an object in ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$. Our goal is to give an intrinsic description of the homologically perfect objects in ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ that does not depend on the chosen t-structure. For affine schemes, this has already been observed in Lemma 5.3, but the non-affine case is more complicated and relies crucially on Neeman’s work on approximability [33, 34]. The main result is:

Theorem B.1

Let ${\mathbb {X}}$ be a separated noetherian scheme. An object $X\in {\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ belongs to ${\mathbf {D}}^b({\text {coh }}{\mathbb {X}})$ if and only if X is the homotopy colimit of a sequence $X_0 \rightarrow X_1 \rightarrow X_2 \rightarrow \cdots$ of perfect complexes on ${\mathbb {X}}$ satisfying the following conditions for every $C \in {\mathbf {D}}^\mathrm {per}({\mathbb {X}})$:

• (1) ${\text {Hom}}(C,X_s) \xrightarrow {_\sim }{\text {Hom}}(C,X_{s+1})$ for $s \gg 0$, and

• (2) ${\text {Hom}}(C,\Sigma ^nX) = 0$ for $|n |\gg 0$.

Before we give the proof of the theorem at the end of this appendix, we record the following consequence, which is an immediate application of Proposition 8.1 and Theorem B.1. It shows in particular that the completion

$$\begin{aligned} \widehat{{\mathbf {D}}^\mathrm {per}({\mathbb {X}})}^b\xrightarrow {\ _\sim \ }{\mathbf {D}}^b({\text {coh }}{\mathbb {X}}) \end{aligned}$$

depends only on the triangulated structure of ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$.

Corollary B.2

The homologically perfect objects on a separated noetherian scheme ${\mathbb {X}}$ with respect to the standard t-structure depend only on the triangulated structure of ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$. $\square$

We will prepare for the proof of the theorem with three lemmata which make use of Neeman’s study of strong generators and approximability for triangulated categories.

Lemma B.3

Let $i:{\mathbb {U}}\rightarrow {\mathbb {X}}$ be an open immersion. If $(X_s)_s$ is a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$, then $(i^*X_s)_s$ is a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {U}})$.

Proof

First note that, because i is an open immersion and thus automatically quasi-compact, $i^*$ exhibits ${\mathbf {D}}({\text {Qcoh }}{\mathbb {U}})$ as the essential image of a smashing Bousfield localisation on ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$. Therefore, $i^*$ preserves homotopy colimits and compact object and it has a fully faithful right adjoint ${\mathbf {R}}{i}_*$. In particular, $i^*G_{\mathbb {X}}$ is a compact generator of ${\mathbf {D}}({\text {Qcoh }}{\mathbb {U}})$, which we will denote by $G_{\mathbb {U}}$. Moreover, it follows from the projection formula that for every $Y \in {\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ there is a canonical quasi-isomorphism

$$\begin{aligned} {\mathbf {R}}{i}_*i^*Y \simeq ({\mathbf {R}}{i}_*{\mathcal {O}}_{\mathbb {U}}) \otimes ^{{\mathbf {L}}}Y, \end{aligned}$$

(B.1)

where ${\mathcal {O}}_{\mathbb {U}}$ is the structure sheaf of ${\mathbb {U}}$.

In order to prove the lemma, it suffices by Lemma 5.2 to show that for every $k \in {\mathbb {Z}}$ there exists an s(k) such that for all $s>s(k)$:

$$\begin{aligned} {\text {Hom}}(\Sigma ^kG_{\mathbb {U}}, i^*X_s) \xrightarrow {_\sim }{\text {Hom}}(\Sigma ^kG_{\mathbb {U}}, i^*X_{s+1}). \end{aligned}$$

Without loss of generality, we will demonstrate the existence of s(0); the remaining cases follow by an analogous argument applied to the shifts of $G_{\mathbb {U}}$. By adjunction, choice of $G_{\mathbb {U}}= i^*G_{\mathbb {X}}$, and substituting (B.1), we thus have to show that there exists an integer s(0) such that for all $s> s(0)$ and ${\mathcal {F}}= {\mathbf {R}}{i}_*{\mathcal {O}}_{\mathbb {U}}\in {\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$:

$$\begin{aligned} {\text {Hom}}(G_{{\mathbb {X}}}, {\mathcal {F}}\otimes ^{{\mathbf {L}}}X_s) \xrightarrow {_\sim }{\text {Hom}}(G_{{\mathbb {X}}}, {\mathcal {F}}\otimes ^{{\mathbf {L}}}X_{s+1}). \end{aligned}$$

(B.2)

Note that the class of objects ${\mathcal {F}}\in {\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ for which (B.2) holds is closed under retracts and arbitrary direct sums as $G_{\mathbb {X}}$ is compact and $\otimes ^{{\mathbf {L}}}$ commutes with direct sums.

The object ${\mathcal {O}}_{\mathbb {U}}$ is perfect on U, so we may invoke Neeman’s result [33, Thm. 0.18]: there exist $A_0,B_0,N_0$ with $A_0 \le B_0$ such that ${\mathbf {R}}{i}_*{\mathcal {O}}_{\mathbb {U}}\in \overline{\langle {G_{\mathbb {X}}}\rangle }_{N_0}^{A_0,B_0}$, i.e., ${\mathbf {R}}{i}_*{\mathcal {O}}_{\mathbb {U}}$ can be built from the collection $(\Sigma ^k G_{\mathbb {X}})_{A_0\le k \le B_0}$ using direct sums, retracts, and at most $N_0$ extensions; we refer to [33] for the precise definition of $\overline{\langle {G_{\mathbb {X}}}\rangle }_{N}^{A,B}$. For ${\mathcal {F}}= \Sigma ^kG_{\mathbb {X}}$ and writing $G_{{\mathbb {X}}}^{\vee }$ for the dual of $G_{{\mathbb {X}}}$, the Cauchy property applied to $C = G_{{\mathbb {X}}} \otimes ^{{\mathbf {L}}}\Sigma ^{-k}G_{{\mathbb {X}}}^{\vee }$ provides an integer $t_k$ such that for all $s>t_k$ there is an isomorphism

$$\begin{aligned} {\text {Hom}}(G_{{\mathbb {X}}} \otimes ^{{\mathbf {L}}}\Sigma ^{-k}G_{{\mathbb {X}}}^{\vee }, X_s) \xrightarrow {_\sim }{\text {Hom}}(G_{{\mathbb {X}}} \otimes ^{{\mathbf {L}}}\Sigma ^{-k}G_{{\mathbb {X}}}^{\vee }, X_{s+1}). \end{aligned}$$

Set $f(1,A,B) = \max \{t_k\mid k \in [A,B]\}$, then (B.2) holds for all $s>f(1,A,B)$ and ${\mathcal {F}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{1}^{A,B}$.

We will proceed by induction on N, proving the following claim: for any $N \ge 1$ and any $A\le B$ there exists an integer f(N, A, B) such that for all $s>f(N,A,B)$ and ${\mathcal {F}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{N}^{A,B}$ there is an isomorphism

$$\begin{aligned} {\text {Hom}}(G_{{\mathbb {X}}}, {\mathcal {F}}\otimes ^{{\mathbf {L}}}X_s) \xrightarrow {_\sim }{\text {Hom}}(G_{{\mathbb {X}}}, {\mathcal {F}}\otimes ^{{\mathbf {L}}}X_{s+1}). \end{aligned}$$

This will then imply the existence of $s(0):=f(N_0,A_0,B_0)$.

We have just checked that the claim holds for $N=1$ and arbitrary $A\le B$. Assume the claim has been proven for $N \ge 1$ and let ${\mathcal {F}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{N+1}^{A,B}$, i.e., ${\mathcal {F}}$ is a retract of an object ${\mathcal {F}}'$ which fits in a triangle

$$\begin{aligned} {\mathcal {E}}\longrightarrow {\mathcal {F}}' \longrightarrow {\mathcal {G}}\longrightarrow \Sigma {\mathcal {E}}\end{aligned}$$

with ${\mathcal {E}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{1}^{A,B}$ and ${\mathcal {G}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{N}^{A,B}$. We thus obtain a morphism of exact sequences

Note that $\Sigma ^{-1}{\mathcal {G}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{N}^{A-1,B-1}$ and $\Sigma {\mathcal {E}}\in \overline{\langle {G_{{\mathbb {X}}}}\rangle }_{1}^{A+1,B+1}$. Therefore, if we set

$$\begin{aligned} f(N+1,A,B) = \max \{f(1,A,B),f(1,A+1,B+1),f(N,A,B),f(N,A-1,B-1)\}, \end{aligned}$$

then the morphisms $\alpha _1, \alpha _2, \alpha _4, \alpha _5$ in the above diagram are isomorphisms, hence so is $\alpha _3$ by the five lemma. Consequently, $f(N+1,A,B)$ has the desired properties, and we conclude by induction. $\square$

Lemma B.4

If $X \in {\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ is the homotopy colimit of a Cauchy sequence $(X_s)_s$ in ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$, then X has coherent cohomology sheaves.

Proof

Suppose ${\mathbb {U}}$ is an open affine subscheme of ${{\mathbb {X}}}$ and denote by $i:{\mathbb {U}}\rightarrow {{\mathbb {X}}}$ the corresponding inclusion. By Lemma B.3, $(i^*X_s)_s$ is a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {U}})$, so for any n the sequence

$$\begin{aligned} (H^n(i^*X_s))_s \cong ({\text {Hom}}(\Sigma ^{-n}{\mathcal {O}}_{{\mathbb {U}}},X_s))_s \end{aligned}$$

stabilises for $s \gg 0$, where the isomorphism is because ${\mathbb {U}}$ is affine. It follows that the homotopy colimit $i^*X$ of $(i^*X_s)_s$ has coherent cohomology. Since coherence is a local property, the cohomology sheaves of X are coherent. $\square$

Next we identify the objects having bounded cohomology, using the following criterion. We are grateful to Amnon Neeman for suggesting a proof.

Lemma B.5

An object X in ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$ belongs to ${\mathbf {D}}^b({\text {Qcoh }}{\mathbb {X}})$ if and only if for all compact C we have ${\text {Hom}}(C,\Sigma ^nX)=0$ for $|n|\gg 0$.

Proof (Neeman)

Fix a compact generator $G=G_{\mathbb {X}}$ and an object X in ${\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$.

If X is in ${\mathbf {D}}^b({\text {Qcoh }}{\mathbb {X}})$, then the fact that ${\text {Hom}}(G,\Sigma ^nX)=0$ for $|n|\gg 0$ is standard; see [39, §09M2].

If ${\text {Hom}}(G,\Sigma ^nX)=0$ for $n\gg 0$, then X is in ${\mathbf {D}}^-({\text {Qcoh }}{\mathbb {X}})$, by [25, Thm. 4.2].

Set ${\mathcal {T}}:={\mathbf {D}}({\text {Qcoh }}{\mathbb {X}})$. The object G generates a t-structure by setting for $n\in {\mathbb {Z}}$

$$\begin{aligned} {\mathcal {T}}_G^{>n}&:=\{X\in {\mathcal {T}}\mid {\text {Hom}}(G,\Sigma ^i X)=0\text { for all } i\le n\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {T}}_G^{\le n}&:=\{X\in {\mathcal {T}}\mid {\text {Hom}}(X,{\mathcal {T}}_G^{>n})=0\}. \end{aligned}$$

It follows from [34, Ex. 3.6] that this t-structure is equivalent to the standard t-structure on ${\mathcal {T}}$ in the following sense: there exist $p\ge q$ in ${\mathbb {Z}}$ such that

$$\begin{aligned} {\mathcal {T}}_G^{>p}\subseteq {\mathcal {T}}^{>0}\subseteq {\mathcal {T}}_G^{>q}. \end{aligned}$$

Thus ${\text {Hom}}(G,\Sigma ^nX)=0$ for $n\ll 0$ implies

$$\begin{aligned} X\in \bigcup _{n\in {\mathbb {Z}}}{\mathcal {T}}_G^{>n}= \bigcup _{n\in {\mathbb {Z}}}{\mathcal {T}}^{>n}={\mathbf {D}}^+({\text {Qcoh }}{\mathbb {X}}). \end{aligned}$$

Note that the proof in [34] requires the scheme to be quasi-compact and separated. $\square$

Proof of Theorem B.1

First assume that X belongs to ${\mathbf {D}}^b({\text {coh }}{\mathbb {X}})$. Then the implication (1) $\Rightarrow$ (3) of Proposition 8.1 shows that X can be written as the homotopy colimit of a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$, keeping in mind the comments about pseudo-coherent objects before Proposition 8.1. Condition (2) follows from Lemma B.5.

Conversely, suppose X is the homotopy colimit of a Cauchy sequence in ${\mathbf {D}}^\mathrm {per}({\mathbb {X}})$ satisfying Condition (2). It follows from Lemma B.5 that X has bounded cohomology, while Lemma B.4 guarantees that X has coherent cohomology sheaves, hence X belongs to ${\mathbf {D}}^b({\text {coh }}{\mathbb {X}})$. $\square$

Appendix C: Morphic enhancements and triangle completions

by Bernhard Keller

For a category ${\mathcal {C}}$, we denote by ${\mathcal {M}}{\mathcal {C}}$ the category of morphisms $f:X_1 \rightarrow X_0$ of ${\mathcal {C}}$. Let ${\mathcal {A}}$ be an abelian category and ${\mathcal {D}}{\mathcal {A}}$ its derived category. We have the cone functor

$$\begin{aligned} {\mathcal {D}}{\mathcal {M}}{\mathcal {A}}\rightarrow {\mathcal {D}}{\mathcal {A}}\end{aligned}$$

taking a morphism of complexes f to its mapping cone. It allows us to capture the notion of standard triangle and of coherent morphism between standard triangles. In this appendix, we recall the axiomatization of the links between ${\mathcal {D}}{\mathcal {M}}{\mathcal {A}}$ and ${\mathcal {D}}{\mathcal {A}}$ given in Sect. 6 of [19] and apply it to the construction of triangulated completions of triangulated categories. Our treatment is slightly different from that of [19] because we work with triangulated categories instead of suspended categories.

1.1 Morphic enhancements

Let ${\mathcal {T}}$ and ${\mathcal {T}}_1$ be triangulated categories and

$$\begin{aligned} Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1 \end{aligned}$$

a fully faithful triangle functor admitting a left adjoint $P_0$ and a right adjoint $P_1$. We define an additive functor

$$\begin{aligned} M:{\mathcal {T}}_1 \rightarrow {\mathcal {M}}{\mathcal {T}}\; , \; X \mapsto MX=(\alpha X:P_1 X \rightarrow P_0 X) \end{aligned}$$

by requiring that $Q_0 \alpha X$ equals the composition of the adjunction morphisms

$$\begin{aligned} Q_0 P_1 X \rightarrow X \rightarrow Q_0 P_0 X. \end{aligned}$$

For example, with the above notations, we can take ${\mathcal {T}}={\mathcal {D}}{\mathcal {A}}$ and ${\mathcal {T}}_1={\mathcal {D}}{\mathcal {M}}{\mathcal {A}}$. We identify the objects of ${\mathcal {D}}{\mathcal {M}}{\mathcal {A}}$ with morphisms of complexes. With this convention, the functor $Q_0$ takes a complex X to its identity morphism and the functors $P_i$ take a morphism of complexes $f:X_1 \rightarrow X_0$ to $X_i$, $i=0,1$. Then the functor $M:{\mathcal {D}}{\mathcal {M}}{\mathcal {A}}\rightarrow {\mathcal {M}}{\mathcal {D}}{\mathcal {A}}$ takes a morphism of complexes $f:X_1 \rightarrow X_0$ to its image in the category of morphisms of the derived category ${\mathcal {D}}{\mathcal {A}}$ (each morphism of complexes yields a morphism in the derived category).

Recall that the triple $(P_0, Q_0, P_1)$ yields a canonical recollement [1]

Recall that a functor is an epivalence if it is conservative (i.e. it detects isomorphisms), full and essentially surjective.

Theorem C.1

The following are equivalent:

• (i) The functor $M:{\mathcal {T}}_1 \rightarrow {\mathcal {M}}{\mathcal {T}}$ is an epivalence.

• (ii) In the above recollement, we have ${\text {Ker }}P_0\subseteq ({\text {Ker }}P_1)^\perp$ and the composition $P_1 Q_1'$ is an equivalence.

Definition C.2

The triangle functor $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ is a morphic enhancement of ${\mathcal {T}}$ if the equivalent conditions of the theorem hold.

For example, it is easy to check that the functor $M:{\mathcal {D}}{\mathcal {M}}{\mathcal {A}}\rightarrow {\mathcal {M}}{\mathcal {D}}{\mathcal {A}}$ is an epivalence if ${\mathcal {A}}$ is an abelian category. For more examples, we refer to Sect. C.2 below.

Proof

We prove the implication from (i) to (ii). We start by constructing a right adjoint $P_{1\rho }$ of $P_1$. Let Y be an object of ${\mathcal {T}}$. Since M is an epivalence, we can find an object $P_{1\rho }Y$ and an isomorphism in ${\mathcal {M}}{\mathcal {T}}$

For X in ${\mathcal {T}}_1$, consider the map

$$\begin{aligned} {\mathcal {T}}_1(X,P_{1\rho } Y) \rightarrow {\mathcal {T}}(P_1X,Y) \end{aligned}$$

taking f to $(\phi Y)(P_1 f)$. Since M is full, it is surjective. Suppose that $f:X \rightarrow P_{1\rho } Y$ is in the kernel. Form a triangle

Its image under M is the morphism of triangles

This shows that Mg admits a retraction in ${\mathcal {M}}{\mathcal {T}}$. Since M is full and conservative, this implies that g admits a retraction and f vanishes. Thus we have the right adjoint $P_{1\rho }$ of $P_1$. Since $P_1$ is a localization functor, $P_{1\rho }$ is fully faithful. By construction, its image is ${\text {Ker }}P_0$. Therefore, the functors $P_1$ and $P_{1\rho }$ induce quasi-inverse equivalences between ${\mathcal {T}}$ and ${\text {Ker }}P_0$. We also know that $Q_1'$ and $P_2'$ induce quasi-inverse equivalences between ${\mathcal {T}}_1/{\mathcal {T}}$ and ${\text {Ker }}P_0$. Thus, the functor $P_1 Q_1'$ is an equivalence. Now let X be in ${\text {Ker }}P_1$, Y in ${\text {Ker }}P_0$ and let $f:X\rightarrow Y$ be a morphism. Form a triangle

Its image under M is the morphism of triangles

It follows that Mg admits a retraction. Since M is full and conservative, g admits a retraction and f vanishes.

We prove the implication from (ii) to (i). Let X be in ${\mathcal {T}}_1$ and Y in ${\mathcal {T}}$. We have

$$\begin{aligned} {\mathcal {T}}(P_1 X,Y) \xrightarrow {_\sim }{\mathcal {T}}(P_1 X, P_1 Q_1' (P_1 Q_1')^{-1} Y) \xrightarrow {_\sim }{\mathcal {T}}(Q_0 P_1 X, Q_1' (P_1Q'_1)^{-1}Y). \end{aligned}$$

We have the triangle

Since there are no nonzero morphisms from ${\text {Ker }}P_1 = {\text {Im }}Q_2'$ to ${\text {Ker }}P_0={\text {Im }}Q_1'$, it follows that we have a bijection

$$\begin{aligned} {\mathcal {T}}(P_1 X,Y) \xrightarrow {_\sim }{\mathcal {T}}(X, Q_1' (P_1 Q_1')^{-1} Y). \end{aligned}$$

Thus, the functor $P_1$ admits the right adjoint $Q_1=Q_1' (P_1 Q_1')^{-1}$. Since $P_1$ is a localization functor, $Q_1$ is fully faithful. We have ${\text {Im }}Q_1 ={\text {Im }}Q_1' ={\text {Ker }}P_0$. We prepare for the proof of the fullness of M. Let X be in ${\mathcal {T}}_1$. We form the triangle

(C.2)

over the morphism whose components are the adjunction morphisms. The adjunctions yield a canonical isomorphism

$$\begin{aligned} P_1 Q_0 P_0 X \oplus P_1 Q_1 P_1 X \xrightarrow {_\sim }P_0 X \oplus P_1 X. \end{aligned}$$

Using this we see that the image of the triangle (C.2) under M is the morphism of triangles

In particular, Y belongs to ${\text {Ker }}P_0$ and $\beta :P_0 X \xrightarrow {_\sim }P_1 Y$ yields a canonical isomorphism $Q_1 P_0 X \xrightarrow {_\sim }Y$. Thus the triangle (C.2) is isomorphic to a functorial triangle

(C.3)

Let Z be in ${\mathcal {T}}_1$. If we apply ${\mathcal {T}}_1(Z,?)$ to this triangle and use the adjunctions, we obtain a bifunctorial exact sequence

This shows in particular that $M:{\mathcal {T}}_1 \rightarrow {\mathcal {M}}{\mathcal {T}}_0$ is full. We claim that its kernel is an ideal of square 0. Indeed, suppose that $g:X \rightarrow Y$ and $f:Y\rightarrow Z$ belong to the kernel. Consider the morphisms of triangles

Clearly g factors through $\Sigma ^{-1}Q_1 P_0 Y \rightarrow Y$ and f factors through

$$\begin{aligned} Y \rightarrow Q_0 P_0 Y\oplus Q_1 P_1 Y. \end{aligned}$$

It follows that fg vanishes. Since M is full, it follows that it is conservative. Let us show that it is essentially surjective. Let $f:X_1 \rightarrow X_0$ be an object of ${\mathcal {M}}{\mathcal {T}}$ and consider the componentwise split short exact sequence of ${\mathcal {M}}{\mathcal {T}}$

The middle and the right hand term lift respectively to $Q_1 X_1 \oplus Q_0 X_0$ and $Q_1 X_0$. Since M is full, the morphism between the middle and the right hand term lifts to a morphism $g:Q_1 X_1 \oplus Q_0 X_0 \rightarrow Q_1 X_0$. It is easy to see that $f:X_1 \rightarrow X_0$ is isomorphic to MY, where Y is defined by the triangle

$\square$

1.2 Examples

As we have already seen, if ${\mathcal {A}}$ is abelian, then the derived category ${\mathcal {D}}{\mathcal {M}}{\mathcal {A}}$ yields a morphic enhancement of ${\mathcal {D}}{\mathcal {A}}$.

More generally, if ${\mathcal {T}}$ is an algebraic triangulated category, i.e. triangle equivalent to the stable category $\underline{{\mathcal {E}}}$ of a Frobenius category ${\mathcal {E}}$, then it admits a morphic enhancement given by the functor

$$\begin{aligned} X \mapsto ({\text {id }}:X \rightarrow X) \end{aligned}$$

from $\underline{{\mathcal {E}}}$ to the stable category $\underline{{\mathcal {I}}{\mathcal {E}}}$ of the category ${\mathcal {I}}{\mathcal {E}}$ of inflations $X_1 \rightarrow X_0$ of ${\mathcal {E}}$ endowed with the class of short exact sequences inducing conflations in the two components and in the cokernel, cf. Example b) of Sect. 6.1 in [19].

More generally, if ${\mathcal {T}}$ is the base category of a (strong) stable derivator $\mathbb {D}$ in the sense of [13], then the value of $\mathbb {D}$ on the index category $\{0<1\}$ yields a morphic enhancement of ${\mathcal {T}}$. Since the homotopy category of each combinatorial stable model category is the base of a stable derivator (cf. [8, 13]), the triangulated categories arising commonly in algebra and topology admit morphic enhancements.

More generally, if ${\mathcal {T}}$ is the base of an epivalent tower of triangulated categories in the sense of [19], then ${\mathcal {T}}$ has a morphic enhancement given by the first floor of the tower.

1.3 Properties

Let $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ be a morphic enhancement in the sense of Sect. C.1. Part b) of the following proposition shows that the underlying additive categories of ${\mathcal {T}}$ and ${\mathcal {T}}_1$ and the additive functor $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ determine the triangulated structure of ${\mathcal {T}}$.

Proposition C.3

• (a) There is an infinite sequence of adjoint functors

  $$\begin{aligned} \ldots \dashv P_n \dashv Q_n \dashv P_{n+1} \dashv Q_{n+1} \dashv \ldots \ , n\in \mathbb {Z}. \end{aligned}$$

  We have natural isomorphisms $\Sigma Q_n \xrightarrow {_\sim }Q_{n+3}$ and $\Sigma P_n \xrightarrow {_\sim }P_{n-3}$ for all integers n. Each $Q_n:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ is a morphic enhancement with associated recollement

  

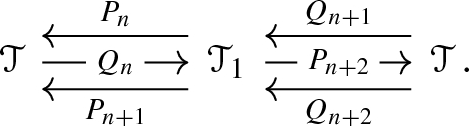
• (b) We have a canonical isomorphism $\Sigma \xrightarrow {_\sim }P_{-1} Q_1$. For each $X\in {\mathcal {T}}_1$, there is a functorial triangle

  

  where the first two morphisms are given by the adjunctions and the third one is the composition

  $$\begin{aligned} P_{-1} X \rightarrow P_{-2} X \xrightarrow {_\sim }\Sigma P_1 X. \end{aligned}$$

  Each triangle of ${\mathcal {T}}$ is isomorphic to a triangle of this form.

• (c) The kernel of $M:{\mathcal {T}}_1 \rightarrow {\mathcal {M}}{\mathcal {T}}$ is an ideal of square zero. For $X,Y\in {\mathcal {T}}_1$, there is a bifunctorial exact sequence

  $$\begin{aligned} {\mathcal {T}}(\Sigma P_1 X, P_0 Y) \rightarrow {\mathcal {T}}_1(X,Y) \rightarrow {\mathcal {M}}{\mathcal {T}}(MX,MY) \rightarrow 0. \end{aligned}$$

Proof

• (a) In the proof of Theorem C.1, we have constructed the adjoint $Q_1$ as $Q_1' (P_1 Q_1')^{-1}$. Since $P_1 Q_1'$ is an equivalence and $Q_1'$ admits the right adjoint $P_2'$, the functor $Q_1$ admits a right adjoint $P_2$. We have ${\text {Im }}Q_1 = {\text {Ker }}P_0$. Whence a short exact sequence

  

  and a recollement

  

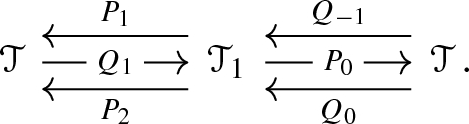
  We need to show that $Q_1:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ is a morphic enhancement. We have ${\text {Ker }}P_2={\text {Im }}Q_0$ and for $X\in {\mathcal {T}}$ and $Y\in {\text {Ker }}P_1$, we have

  $$\begin{aligned} {\mathcal {T}}_1(Q_0 X,Y) \xrightarrow {_\sim }{\mathcal {T}}(X,P_1 Y)=0. \end{aligned}$$

  Thus, we have ${\text {Ker }}P_1 \subseteq ({\text {Ker }}P_2)^\perp$. We need to check that $P_2 Q_{-1}$ is an equivalence. For $X\in {\mathcal {T}}$, we have the triangle

  

  By applying $P_1$ to this triangle we find the triangle

  

  and therefore we have $X \xrightarrow {_\sim }\Sigma P_2 Q_{-1} X$. Therefore, the functor $P_2 Q_{-1}:{\mathcal {T}}\rightarrow {\mathcal {T}}$ is an equivalence isomorphic to $\Sigma ^{-1}$. Thus, the functor $Q_1:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ is a morphic enhancement. By induction, we get a sequence of adjoints

  $$\begin{aligned} P_0 \dashv Q_0 \dashv P_1 \dashv Q_1 \dashv \ldots \dashv P_n \dashv Q_n \dashv \ldots \ . \end{aligned}$$

  Since our assumption is self-dual, we also get a sequence of adjoints

  $$\begin{aligned} \ldots \dashv P_{-n} \dashv Q_{-n} \dashv \ldots \dashv P_0 \dashv Q_0. \end{aligned}$$

  We have already constructed an isomorphism $P_2 Q_{-1} \xrightarrow {_\sim }\Sigma ^{-1}$ and we have $\Sigma ^{-1} \xrightarrow {_\sim }P_2 \Sigma ^{-1} Q_2$. Whence an isomorphism $P_2 \Sigma Q_{-1} \xrightarrow {_\sim }P_2 Q_2$. We have ${\text {Im }}Q_{-1} = {\text {Ker }}P_1 \subseteq ({\text {Ker }}P_2)^\perp$. By the recollement

  

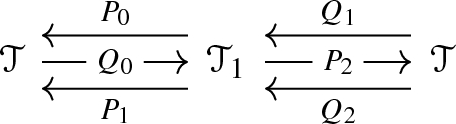
  we also have ${\text {Im }}Q_2 ={\text {Ker }}P_1 \subseteq ({\text {Ker }}P_2)^\perp$. Since the restriction of $P_2$ to $({\text {Ker }}P_2)^\perp$ is an equivalence, we get an isomorphism $\Sigma Q_{-1} \xrightarrow {_\sim }Q_2$. By induction, we get $\Sigma Q_n \xrightarrow {_\sim }Q_{n+3}$ and by adjunction $\Sigma ^{-1} P_n \xrightarrow {_\sim }P_{n+3}$ for all integers n.

• (b) We have seen in the proof of a) that there is a canonical isomorphism $P_2 Q_{-1} \xrightarrow {_\sim }\Sigma ^{-1}$. By passing to the left adjoints we get an isomorphism $Q_1 P_{-1} \xrightarrow {_\sim }\Sigma$. As it follows from the proof of a), we have a recollement

  

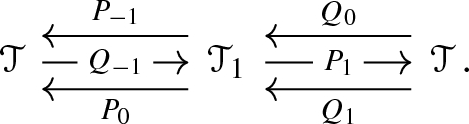
  Thus, for $X\in {\mathcal {T}}_1$, we have the functorial triangle

  

  By applying $P_0$ to this triangle we get the functorial triangle

  

  Since M is essentially surjective, each triangle of ${\mathcal {T}}$ is isomorphic to a triangle of this form.

• (c) This was already shown in the proof of the implication from (ii) to (i) in Theorem C.1.

$\square$

We keep the assumptions on $Q_0 :{\mathcal {T}}\rightarrow {\mathcal {T}}_1$.

Definition C.4

A standard triangle is a triangle of ${\mathcal {T}}$

associated with an object X of ${\mathcal {T}}_1$. A coherent morphism between standard triangles is a morphism

induced by a morphism $X \rightarrow Y$ of ${\mathcal {T}}_1$.

The following lemma will be crucial in checking the axioms of a triangulated category for a completion.

Lemma C.5

Let $f:X \rightarrow Y$ be a morphism of ${\mathcal {T}}_1$. Let

$$\begin{aligned} X'=Q_{-1}P_{-1}X \oplus Q_0 P_0 X\oplus Q_1 P_1 X \end{aligned}$$

and let $f':X \rightarrow Y\oplus X'$ be the morphism whose components are f and the adjunction morphisms. Let

be a triangle. Then the standard triangle

is isomorphic to the mapping cone [32, Sect. 1.3] over the morphism of triangles

Proof

For an object X of ${\mathcal {T}}_1$, let

be the standard triangle and let TX be the complex obtained by glueing the following triangles along their boundaries

where $\alpha _p X=(-1)^p \Sigma ^p \alpha X$, $\beta _p X=(-1)^p \Sigma ^p \beta X$ and $\gamma _p X = (-1)^p \Sigma ^p \gamma X$. We have to show that TZ is isomorphic to the mapping cone over the morphism $Tf:TX \rightarrow TY$. For a complex $C=(C^p,d^p)$, let IC be the complex with components $C^p\oplus C^{p+1}$ and the differential

$$\begin{aligned} \left[ {\begin{matrix}0 &{} {\text {id }}\\ 0 &{} 0\end{matrix}}\right] :C^p \oplus C^{p+1} \rightarrow C^{p+1}\oplus C^{p+2} \end{aligned}$$

and let $i_C:C \rightarrow IC$ be the morphism of complexes with the components

$$\begin{aligned} \left[ {\begin{matrix}{\text {id }}\\ d^p\end{matrix}}\right] :C^p \rightarrow C^p\oplus C^{p+1}. \end{aligned}$$

One checks easily that $TX'$ is canonically isomorphic to ITX and that the morphism $X \rightarrow X'$ whose components are the adjunction morphisms induces the morphism $i_{TX}:TX \rightarrow ITX$. Thus, the morphism $f:X \rightarrow Y\oplus X'$ induces the morphism

$$\begin{aligned} \left[ {\begin{matrix}Tf \\ i_{TX}\end{matrix}}\right] :TX \rightarrow TY\oplus ITX. \end{aligned}$$

Notice that this is a componentwise split monomorphism whose cokernel is canonically isomorphic to the mapping cone over $Tf:TX \rightarrow TY$. Now the triangle

yields a componentwise split exact sequence

It follows that TZ is canonically isomorphic to the cone over Tf. $\square$

1.4 Morphic functors, compact objects

Let $Q_0:{\mathcal {S}}\rightarrow {\mathcal {S}}_1$ and $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ be morphic enhancements. A morphic functor ${\mathcal {S}}\rightarrow {\mathcal {T}}$ is given by a square of triangle functors

commutative up to given isomorphism such that the canonical morphisms

$$\begin{aligned} P_0 F_1 \rightarrow F P_0 \quad \text {and}\quad FP_1 \rightarrow P_1 F_1 \end{aligned}$$

are invertible. Examples of morphic functors are provided by morphisms of epivalent towers of triangulated categories [19] and by morphisms of stable derivators [13].

Lemma C.6

If $F:{\mathcal {S}}\rightarrow {\mathcal {T}}$ is a morphic functor, we have canonical isomorphisms

$$\begin{aligned} P_n F_1 \xrightarrow {_\sim }F P_n \quad \text {and}\quad Q_n F \xrightarrow {_\sim }F_1 Q_n \end{aligned}$$

for all integers n.

Proof

Since $Q_{-1}:{\mathcal {S}}\rightarrow {\mathcal {S}}_1$ and $Q_{-1}:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ are again morphic enhancements, it is enough to show the claim for $Q_{-1}$ and $P_{-1}$. Indeed, by induction it will then follow for $Q_n$ and $P_n$ for all $n<0$ and by duality for all $n\ge 0$. The image of the canonical morphism $Q_{-1} F \rightarrow F_1 Q_{-1}$ under $P_0$ fits into the commutative square

Thus, it is invertible. The image of $Q_{-1} F \rightarrow F_1 Q_{-1}$ under $P_1$ is the identity of the zero object. Since M is conservative, it follows that the morphism $Q_{-1} F \rightarrow F_1 Q_{-1}$ is invertible. Now consider the canonical morphism

$$\begin{aligned} P_{-1} F_1 \rightarrow F P_{-1}. \end{aligned}$$

For each X of ${\mathcal {S}}_1$, it fits into a morphism of triangles

Thus, it is invertible. $\square$

The inclusion of the subcategory of compact objects in a compactly generated triangulated category with a morphic enhancement is an example of a morphic functor, as shown by the next lemma.

Lemma C.7

Let $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ be a morphic enhancement. Then ${\mathcal {T}}$ is compactly generated if and only if ${\mathcal {T}}_1$ is compactly generated. In this case, an object X of ${\mathcal {T}}_1$ is compact if and only if $P_0 X$ and $P_1 X$ are compact and the functor $Q_0$ induces a morphic enhancement ${\mathcal {T}}^c \rightarrow {\mathcal {T}}_1^c$, where ${\mathcal {T}}^c$ is the subcategory of compact objects. Moreover, the inclusion ${\mathcal {T}}^c \rightarrow {\mathcal {T}}$ is a morphic functor.

Proof

The localization functor $P_1:{\mathcal {T}}_1 \rightarrow {\mathcal {T}}$ admits two successive right adjoints. Thus it commutes with arbitrary coproducts and preserves compactness. Therefore, if ${\mathcal {T}}_1$ is compactly generated, then so is ${\mathcal {T}}$. For the converse implication, note that all the functors $Q_n$ commute with arbitrary coproducts and preserve compactness (for the same reason). So if ${\mathcal {T}}$ is compactly generated, so are the subcategories ${\text {Im }}Q_0$ and ${\text {Im }}Q_2$ of ${\mathcal {T}}_1$ and their inclusions commute with arbitrary coproducts. Since each object of ${\mathcal {T}}_1$ is an extension of an object of ${\text {Im }}Q_2$ by an object of ${\text {Im }}Q_0$, it follows that ${\mathcal {T}}_1$ has arbitrary coproducts and is generated by the compact objects in ${\text {Im }}Q_2$ and ${\text {Im }}Q_0$. Suppose that ${\mathcal {T}}$ and ${\mathcal {T}}_1$ are compactly generated. The functors $P_1$ and $P_0$ preserve compactness and so do $Q_{-1}$ and $Q_1$. If an object X of ${\mathcal {T}}_1$ has compact $P_0 X$ and $P_1 X$, then it is itself compact because of the triangle

Now suppose that ${\mathcal {T}}$ and ${\mathcal {T}}_1$ are compactly generated. As we have seen, the functor $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ induces a functor $Q_0:{\mathcal {T}}^c \rightarrow {\mathcal {T}}_1^c$ and $P_0$ and $P_1$ induce left and right adjoints. It is now clear that the epivalence $M:{\mathcal {T}}_1 \rightarrow {\mathcal {M}}{\mathcal {T}}$ induces an epivalence $M:{\mathcal {T}}_1^c \rightarrow {\mathcal {M}}{\mathcal {T}}^c$ and that the inclusion ${\mathcal {T}}^c \rightarrow {\mathcal {T}}_1^c$ is a morphic functor. $\square$

1.5 Completion

Let ${\mathcal {T}}$ be a triangulated category with a morphic enhancement $Q_0 :{\mathcal {T}}\rightarrow {\mathcal {T}}_1$. Let ${\mathcal {X}}$ be a class of sequences

$$\begin{aligned} X_0 \rightarrow X_1 \rightarrow \ldots \rightarrow X_p \rightarrow \ldots \end{aligned}$$

of ${\mathcal {T}}$. We assume that the following hold for ${\mathcal {X}}$:

• (a) ${\mathcal {X}}$ is stable under passage to cofinal sequences i.e. if $(X_p)$ belongs to ${\mathcal {X}}$ and $(i_p)$ is a strictly increasing sequence of positive integers, then $(X_{i_p})$ belongs to ${\mathcal {X}}$.

• (b) ${\mathcal {X}}$ is stable under $\Sigma$ and $\Sigma ^{-1}$ i.e. if $(X_p)$ belongs to ${\mathcal {X}}$ so do $(\Sigma X_p)$ and $(\Sigma ^{-1} X_p)$.

• (c) ${\mathcal {X}}$ is stable under cones i.e. if $f:X \rightarrow Y$ is a morphism of sequences of ${\mathcal {X}}$ and for each $p\ge 0$, the object $Z_p$ of ${\mathcal {T}}_1$ lifts the object $f_p :X_p \rightarrow Y_p$ of ${\mathcal {M}}{\mathcal {T}}$ and the morphism $Z_p \rightarrow Z_{p+1}$ lifts the morphism

  

  of ${\mathcal {M}}{\mathcal {T}}$, then the sequence $(P_{-1} Z_p)$ belongs to ${\mathcal {X}}$.

• (d) ${\mathcal {X}}$ is phantomless i.e. for X and Y in ${\mathcal {X}}$, we have

  $$\begin{aligned} {\lim _p}^1 \mathop {\mathrm{colim }}\limits _q {\mathcal {T}}(X_p, Y_q) =0. \end{aligned}$$

Let ${\text {Mod }}{\mathcal {T}}$ be the category of additive functors ${\mathcal {T}}^{\mathrm {op}}\rightarrow \mathrm {Ab}$. For $X\in {\mathcal {T}}$, let $X^\wedge$ be the functor ${\mathcal {T}}(?,X)$ represented by X. Define the completion $\widehat{{\mathcal {T}}_{\mathcal {X}}}$ to be the full subcategory of ${\text {Mod }}{\mathcal {T}}$ whose objects are the colimits

$$\begin{aligned} LX = \mathop {\mathrm{colim }}\limits _p X_p^\wedge \end{aligned}$$

of sequences X of ${\mathcal {X}}$. Note that by Proposition 2.4, this agrees with the definition in the main text. Define $\Sigma :\widehat{{\mathcal {T}}_{\mathcal {X}}} \rightarrow \widehat{{\mathcal {T}}_{\mathcal {X}}}$ to be the functor induced by $X \mapsto \Sigma X$. For a sequence $(Z_p)$ of ${\mathcal {T}}_1$ such that $(P_1 Z_p)$ and $(P_0 Z_p)$ belong to ${\mathcal {X}}$, define the standard triangle associated with Z to be the $\Sigma$–sequence

Thus, the standard triangles of $\widehat{{\mathcal {T}}_{\mathcal {X}}}$ are exactly the colimits of sequences of coherent morphisms between standard triangles of ${\mathcal {T}}$, cf. Definition C.4. Define a triangle of $\widehat{{\mathcal {T}}_{\mathcal {X}}}$ to be a $\Sigma$–sequence isomorphic to a standard triangle.

Theorem C.8

Endowed with the suspension functor $\Sigma$ and the above triangles the completion $\widehat{{\mathcal {T}}_{\mathcal {X}}}$ is a triangulated category. If ${\mathcal {X}}$ contains the constant sequences consisting of identities only, we have a canonical triangle embedding ${\mathcal {T}}\rightarrow \widehat{{\mathcal {T}}_{\mathcal {X}}}$.

Proof

Let X be a sequence in ${\mathcal {X}}$. We need to show that

is a triangle (TR0). In fact, it is the standard triangle associated with the sequence $(Q_0 X_p)$. Let X and Y be sequences in ${\mathcal {X}}$ and let $f:LX \rightarrow LY$ be a morphism. After passing to cofinal sequences we may assume that f is in fact a morphism of sequences. We lift each object $f_p:X_p \rightarrow Y_p$ of ${\mathcal {M}}{\mathcal {T}}$ to an object $Z_p$ of ${\mathcal {T}}_1$ and each morphism

to a morphism $Z_p\rightarrow Z_{p+1}$ of ${\mathcal {T}}_1$. Then the standard triangle associated with $(Z_p)$ yields a triangle whose first morphism identifies with $f:LX \rightarrow LY$ and we have proved TR1. Let

be a commutative diagram of $\widehat{{\mathcal {T}}_{\mathcal {X}}}$ whose rows are triangles. We will show that there is a morphism $LZ \rightarrow LZ'$ completing the diagram to a morphism of triangles whose mapping cone is still a triangle. This implies the rotation axiom TR2 (take $LX'=LY'=LZ'=0$), the axiom about the missing morphism TR3 and axiom TR4’ of Sect. 1.4 of [32]. By Proposition 1.4.6 of [32], the octahedral axiom TR4 follows. We may assume that the given triangles are the standard triangles associated with sequences U and V of ${\mathcal {T}}_1$. The given commutative diagram

is a morphism in ${\mathcal {M}}\widehat{{\mathcal {T}}_{\mathcal {X}}}$. As in Example 2.9, we see that the canonical functor $\widehat{({\mathcal {M}}{\mathcal {T}})_{{\mathcal {M}}{\mathcal {X}}}} \rightarrow {\mathcal {M}}\widehat{{\mathcal {T}}_{\mathcal {X}}}$ is an equivalence, where ${\mathcal {M}}{\mathcal {X}}$ is the class of sequences of morphisms $(X_{1p}\rightarrow X_{0p})$ with $(X_{1p})$ and $(X_{0p})$ in ${\mathcal {X}}$. So the given commutative diagram may be viewed as a morphism

$$\begin{aligned} LMU \rightarrow LMV \end{aligned}$$

in $\widehat{({\mathcal {M}}T)_{{\mathcal {M}}{\mathcal {X}}}}$. We claim that it suffices to lift it to a morphism of sequences $U \rightarrow V$ of ${\mathcal {T}}_1$. Indeed, once we have such a lift, we can form triangles

as in Lemma C.5 and morphisms of triangles

By Lemma C.5, the standard triangle associated with W will be the mapping cone over the morphism of standard triangles associated with $U \rightarrow V$. The given morphism $LMU\rightarrow LMV$ identifies with an element of

$$\begin{aligned} \lim _p \mathop {\mathrm{colim }}\limits _q {\mathcal {M}}{\mathcal {T}}(MU_p, MV_q). \end{aligned}$$

It suffices to show that the natural map

$$\begin{aligned} \lim _p \mathop {\mathrm{colim }}\limits _q {\mathcal {T}}_1(U_p, V_q) \rightarrow \lim _p \mathop {\mathrm{colim }}\limits _q {\mathcal {M}}{\mathcal {T}}(MU_p,MV_q) \end{aligned}$$

is surjective. By part c) of Proposition C.3, for each $p\ge 0$, we have an exact sequence

$$\begin{aligned} \mathop {\mathrm{colim }}\limits _q {\mathcal {T}}(\Sigma P_1 U_p, P_0 V_q) \rightarrow \mathop {\mathrm{colim }}\limits _q {\mathcal {T}}_1(U_p, V_q) \rightarrow \mathop {\mathrm{colim }}\limits _q {\mathcal {M}}{\mathcal {T}}(MU_p, MV_q) \rightarrow 0. \end{aligned}$$

Let us abbreviate it to

$$\begin{aligned} A_p \rightarrow B_p \rightarrow C_p \rightarrow 0. \end{aligned}$$

Let $A'_p$ be the image of $A_p$ in $B_p$. We have the exact sequence

$$\begin{aligned} 0 \rightarrow \lim A'_p \rightarrow \lim B_p \rightarrow \lim C_p \rightarrow {\lim }^1 A'_p. \end{aligned}$$

Since $\lim ^1$ is right exact, we have a surjection $\lim ^1 A_p\rightarrow \lim ^1 A'_p$. Since ${\mathcal {X}}$ is phantomless, the group $\lim ^1 A_p$ vanishes. So

$$\begin{aligned} \lim B_p \rightarrow \lim C_p \end{aligned}$$

is surjective as required. $\square$

1.6 Functoriality

The construction of the completion is functorial with respect to morphic triangle functors. Let us spell this out: Let ${\mathcal {T}}$ and ${\mathcal {T}}'$ be skeletally small triangulated categories and $Q_0 :{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ and $Q_0:{\mathcal {T}}' \rightarrow {\mathcal {T}}'_1$ be morphic enhancements. Let $F:{\mathcal {T}}\rightarrow {\mathcal {T}}'$ be a morphic triangle functor with enhancement $F_1:{\mathcal {T}}_1 \rightarrow {\mathcal {T}}'_1$. Let ${\mathcal {X}}$ and ${\mathcal {X}}'$ be classes of sequences of ${\mathcal {T}}$ and ${\mathcal {T}}'$ satisfying the assumptions of Sect. C.5 and such that $F{\mathcal {X}}\subseteq {\mathcal {X}}'$.

Lemma C.9

The functor F induces a canonical triangle functor $\widehat{F}:\widehat{{\mathcal {T}}_{\mathcal {X}}} \rightarrow \widehat{{\mathcal {T}}'_{{\mathcal {X}}'}}$.

Proof

This is a straightforward verification based on the fact that $(F,F_1)$ is compatible with all the adjoints as checked in Lemma C.6. $\square$

1.7 Completion inside a compactly generated category

Let ${\mathcal {T}}$ be a compactly generated triangulated category with a morphic enhancement $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$. By Lemma C.7, we have an induced morphic enhancement $Q_0:{\mathcal {T}}^c \rightarrow {\mathcal {T}}_1^c$ between the subcategories of compact objects and the inclusion ${\mathcal {T}}^c \rightarrow {\mathcal {T}}$ is morphic. Let ${\mathcal {X}}$ be a class of sequences of ${\mathcal {T}}^c$ satisfying the hypotheses of Sect. C.5. For a sequence X in ${\mathcal {X}}$, we define $\mathop {\mathrm{hocolim }}\limits _p X_p$ as in Sect. 4. As we have seen there, the facts that each sequence $X\in {\mathcal {X}}$ is formed by compact objects and that ${\mathcal {X}}$ is phantomless and stable under $\Sigma$ imply that for X, Y in ${\mathcal {X}}$, we have a canonical bijection

$$\begin{aligned} \widehat{{\mathcal {T}}^c_{\mathcal {X}}}(LX,LY) =\lim _p \mathop {\mathrm{colim }}\limits _q {\mathcal {T}}^c(X_p,Y_q) \xrightarrow {_\sim }{\mathcal {T}}(\mathop {\mathrm{hocolim }}\limits X, \mathop {\mathrm{hocolim }}\limits Y). \end{aligned}$$

Thus we have a fully faithful functor

$$\begin{aligned} F:\widehat{{\mathcal {T}}^c_{\mathcal {X}}} \rightarrow {\mathcal {T}}\end{aligned}$$

taking LX to $\mathop {\mathrm{hocolim }}\limits X$. Clearly, F is endowed with a canonical isomorphism $F\Sigma \xrightarrow {_\sim }\Sigma F$.

Lemma C.10

F is a triangle functor.

Proof

Let

(C.4)

be the standard triangle associated with a sequence X of ${\mathcal {T}}_1^c$ such that $P_0 X$ and $P_1 X$ belong to ${\mathcal {X}}$. Put

$$\begin{aligned} Y=\mathop {\mathrm{hocolim }}\limits _p X_p \end{aligned}$$

in ${\mathcal {T}}_1$. Using the fact that $P_1$, $P_0$ and $P_{-1}$ commute with coproducts, it is easy to see that the standard triangle

is isomorphic to the image of the triangle (C.4) under F. $\square$

1.8 Completions of morphic enhancements

Let ${\mathcal {T}}$ be a triangulated category with a morphic enhancement $Q_0:{\mathcal {T}}\rightarrow {\mathcal {T}}_1$ and let ${\mathcal {X}}$ be a class of sequences of ${\mathcal {T}}$ satisfying the assumptions of Sect. C.5. It is natural to ask whether the triangulated category $\widehat{{\mathcal {T}}_{\mathcal {X}}}$ admits a morphic enhancement given by a completion of ${\mathcal {T}}_1$. Clearly, the class of sequences ${\mathcal {X}}_1$ of ${\mathcal {T}}_1$ needed for this is formed by the sequences X such that $P_1 X$ and $P_0 X$ belong to ${\mathcal {X}}$. Let $Q^j_0:{\mathcal {T}}_1 \rightarrow {\mathcal {T}}_2$, $j=1,2$, be morphic enhancements of ${\mathcal {T}}_1$ such that the categories ${\mathcal {T}}$, ${\mathcal {T}}_1$, ${\mathcal {T}}_2$ together with the given functors and their needed adjoints satisfy the axioms for the first three floors of an epivalent tower of triangulated categories [19]. Then it is not hard to show that ${\mathcal {X}}_1$ satisfies assumptions a), b), and c) of Sect. C.5. We cannot expect that ${\mathcal {X}}_1$ is phantomless in general but this is the case in many examples. Indeed, if ${\mathcal {T}}$ is the perfect derived category of a right coherent ring $\Lambda$, then the canonical morphic enhancement for ${\mathcal {T}}$ is the perfect derived category ${\mathcal {T}}_1$ of the ring $\Lambda _1$ of upper triangular $2\times 2$ matrices over $\Lambda$. Notice that $\Lambda _1$ is still right coherent. If ${\mathcal {X}}$ is the class of bounded Cauchy sequences in ${\mathcal {T}}$, then ${\mathcal {X}}_1$ is easily seen to be the class of bounded Cauchy sequences of ${\mathcal {T}}_1$. So in this example, ${\mathcal {X}}_1$ is still phantomless. We can iterate this process to see that the epivalent tower associated with the bounded derived category of ${\text {mod }}\Lambda$ is the bounded Cauchy completion of the tower associated with the perfect derived category of $\Lambda$. An analogous statement holds for the stable derivators, defined on the 2-category of finite directed categories, associated with the bounded derived category of ${\text {mod }}\Lambda$ and with the perfect derived category of $\Lambda$, cf. the appendix [21] to [26] for these derivators.

Let ${\mathcal {M}}{\mathcal {X}}$ be the class of sequences $(X_{p1} \rightarrow X_{p0})$ of morphisms of ${\mathcal {T}}$ such that $(X_{p1})$ and $(X_{p0})$ belong to ${\mathcal {X}}$.

Lemma C.11

${\mathcal {X}}_1$ is phantomless in ${\mathcal {T}}_1$ if and only if ${\mathcal {M}}{\mathcal {X}}$ is phantomless in ${\mathcal {M}}{\mathcal {T}}$.

Proof

Let X and Y be in ${\mathcal {X}}_1$. By part c) of Lemma C.3, for all $p,q\ge 0$, we have an exact sequence

$$\begin{aligned} {\mathcal {T}}(\Sigma P_1 X_p, P_0 Y_q) \rightarrow {\mathcal {T}}_1(X_p, Y_q) \rightarrow {\mathcal {M}}{\mathcal {T}}(MX_p, MY_q) \rightarrow 0. \end{aligned}$$

We pass to the colimit over q to get an inverse system of exact sequences

$$\begin{aligned} A_p \rightarrow B_p \rightarrow C_p \rightarrow 0. \end{aligned}$$

Since $\lim ^1$ is right exact, it induces an exact sequence

$$\begin{aligned} {\lim }^1 A_p \rightarrow {\lim }^1 B_p \rightarrow {\lim }^1 C_p \rightarrow 0. \end{aligned}$$

Now since ${\mathcal {X}}$ is phantomless, the group $\lim ^1 A_p$ vanishes. $\square$