Abstract
This study aims to investigate the time-dependent squeezing of nanofluid flow, comprising carbon nanotubes of dual nature, e.g. single-walled carbon nanotubes, and multi-walled carbon nanotubes, between two parallel disks. Numerical simulations of the proposed novel model are conducted, accompanied by Cattaneo-Christov heat flux in a Darcy-Forchheimer permeable media. Additional impacts of homogeneous–heterogeneous reactions are also noted, including melting heat. A relevant transformation procedure is implemented for the transition of partial differential equations to the ordinary variety. A computer software-based MATLAB function, bvp4c, is implemented to handle the envisioned mathematical model. Sketches portraying impacts on radial velocity, temperature, and concentration of the included parameters are given, and deliberated upon. Skin friction coefficient and local Nusselt number are evaluated via graphical illustrations. It is observed that the local inertia coefficient has an opposite impact on radial velocity and temperature field. It is further perceived that melting and radiation parameters demonstrate a retarding effect on temperature profile.
Export citation and abstract BibTeX RIS
Nomenclature
| Acronyms | Description |
| MWCNTs | Multi-walled carbon nanotubes |
| MHD | Magnetohydrodynamics |
| SWCNTs | Single-walled carbon nanotubes |
| Symbols | Description |
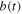
|
Strength of magnetic field |
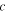
|
Dimensional constant |
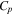
|
Capacity of specific heat |
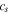
|
Heat capacity of solid surface |
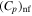
|
Specific heat capacity of nanofluid |
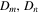
|
Diffusion coefficients |
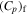
|
Specific heat capacity of fluid |
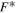
|
Forchheimer parameter |
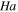
|
Hartmann number |

|
Thermal conductivity of carbon nanotubes |
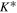
|
Permeability of spongy media |
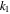
|
Homogeneous reaction parameter |
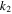
|
Heterogeneous reaction parameter |
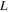
|
Latent heat |
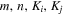
|
Concentrations of chemical species |
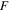
|
Local inertia coefficient |
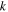
|
Thermal conductivity |
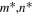
|
Chemical species |

|
Melting heat coefficient |
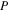
|
Pressure |
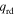
|
Radiative heat flux |
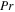
|
Prandtl number |
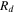
|
Thermal radiation coefficient |

|
Local squeezed Reynolds number |
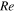
|
Reynolds parameter |
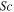
|
Schmidt parameter |
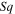
|
Squeeze parameter |
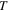
|
Temperature |
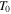
|
Temperature of solid |

|
Temperature at upper disk |
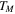
|
Surface temperature |
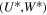
|
Components of velocities |
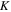
|
Kelvin |
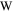
|
Watt |
| Greek symbols | Description |
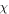
|
Similarity transformation variable |
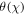
|
Dimensionless temperature |
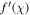
|
Radial velocity (dimensionless velocity) |
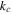
|
Carbon nanotubes thermal conductivity |

|
fluid dynamic viscosity |
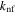
|
Thermal conductivity of nanofluid |
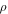
|
Density |

|
Nanofluid density |
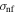
|
Nanofluid electrical conductivity |
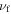
|
Kinematic viscosity of the fluid |
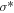
|
Stefan Boltzmann constant |
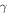
|
Thermal relaxation coefficient |
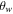
|
Temperature ratio parameter |
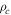
|
Density of carbon nanotubes |
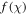
|
Axial velocity (dimensionless velocity) |
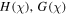
|
Dimensionless concentrations |
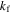
|
Base fluid (water) thermal conductivity |
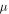
|
dynamic viscosity |

|
Nanofluid dynamic viscosity |

|
Density of fluid |

|
Nanofluid kinematic viscosity |
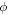
|
Volume fraction of nanoparticles |
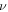
|
Kinematic viscosity |
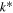
|
Mean absorption coefficient |
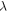
|
Porosity parameter |
| Subscripts | Description |
| 0 | For solid |
| 1 | For homogeneous |
| 2 | For heterogeneous |
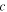
|
Carbon nanotubes |
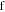
|
Fluid |

|
For upper disk |
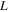
|
For local |
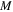
|
For lower disk |

|
Nanofluid |
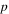
|
Constant pressure |
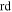
|
Radiative |

|
Solid surface |
Introduction
A carbon nanotube is a large, stretched, thin, and tube-shaped molecule of pure carbon of around 1 to 3 nanometers (1 to 3 billionth of a meter) in breadth (diameter), and 100 to 1000 s of nanometers in length. Iijima [1] introduced the theory of carbon nanotubes at the end of the 20th century, when he discovered some potential applications of CNTs for solar cells, radar-absorbing coating, gas storage, composites, semiconductor devices, ultra-capacitors, etc [2]. CNTs are classified as SWCNTs and MWCNTs. A SWCNT has a regular straw shape with only one layer. A MWCNT is a set of nested SWCNTs of increasing diameters. Din and Khan [3] studied the squeezing flow of Casson fluid with non-linear thermal radiation between parallel disks. Haq et al [4] examined MHD nanofluid squeezed flow based on water with CNTs between 2-parallel disks, and concluded that temperature and velocity profiles increase with high nanoparticle volume fraction. Melting heat in the radiative flow of CNTs with homogeneous–heterogeneous reactions was scrutinized by Hayat et al [5]. They found that the Nusselt number increases for large values of nanoparticle volume fraction.
Recently, squeezed flow between two parallel disks has garnered a great deal of attention, with its vast number of potential applications in technological and industrial systems. Many devices such as stirring pistons in engines, hydraulic brakes, and chocolate filler are based on the flow principle between squeezing regions. Stefan [6] proposed the idea of squeezing flow in 1874. Since then, many researchers have explored the problems associated with squeezing flow. The theoretical investigation regarding squeezing flow between parallel disks is presented by Leider and Bird [7]. Qayyum et al [8] discussed time-dependent squeezing Jeffery fluid flow between two parallel disks. Hayat et al [9] discussed squeezed nanofluid flow-based CNTs, and the impact of thermal radiations on Darcy-Forchheimer spongy media. They posited that an augmentation in nanoparticle volume fraction causes a reduction in both the velocity and the temperature of the fluid. Hashmi et al [10] investigated the analytical simulations for squeezing nanofluid flow amidst parallel disks. It should be noted that these studies are discuss the use of two parallel disks, but do not refer to Cattaneo-Christov heat flux.
The Fourier law of heat conduction has been a criterion benchmark in many practical industries for estimating the behavior of heat transmission. Nevertheless, because of the parabolic-heat equation due to an initial disorder, this system suffers a great deal. Cattaneo [11] tackled this drawback of the Fourier model via the addition of thermal time relaxation. This modification has created a hyperbolic heat equation for the temperature field. Also, within finite speeds, heat transmission is permitted to circulate through thermal waves. Tibullo and Zampoli [12] have worked on innumerable practicable applications i.e. to nanofluid flow, applying the Cattaneo-Christov heat conduction model. Christov [13] posited a modification of the Maxwell-Cattaneo model, which is known as the Cattaneo-Christov thermal flux model. Radiative nanofluid flow with the Cattaneo-Christov heat flux model between parallel disks is studied by Dogonchi et al [14]. Lu et al [15] discussed the mathematical model of unsteady fluid flow containing SWCNTs and MWCNTs under conditions of Cattaneo-Christov heat flux, and homogeneous–heterogeneous reactions between two parallel disks, and determined that temperature rises with an increasing thermal relaxation parameter. Zubair et al [16] discussed the 3D Darcy-Forchheimer squeezing nanofluid flow with Cattaneo-Christov heat flux, using four distinct types of nanoparticles, via the analysis of entropy generation.
Henry Darcy [17] determined the fluid flow over a permeable surface, based on the outcomes of water flow experiments over cribs of sand, and hydro-geology. He defined his idea of fluid flow over a spongy media in 1856. Due to its limitations of small velocity with weaker permeability, Philipps Forchheimer [18] modified the momentum equation by velocity square  within Darcian velocity. This became known as the Forchheimer term, as designated by Muskat [19]. Nasir et al [20] scrutinized the radiative 3D Darcy-Forchheimer flow of carbon nanotubes past a stretchable rotating disk. They posited that fluid velocity falls with an upsurge in inertia and porosity parameters. Jha and Kaurangini [21] presented analytic solutions for Darcy-Forchheimer-based spongy media relations. Kaladhar [22] discussed mixed convection flow with dual stratification effects within a Darcy-Forchheimer medium, finding that velocity is reduced for higher estimates of Darcy-Forchheimer number. A numerical solution for a second law analysis of ferrofluid within a spongy semi annulus is investigated by Sheikholeslami et al [23]. Alamri et al [24] proposed the model of a radiative plane Poiseuille flow of nanofluid, using slip conditions past a porous medium. Some recent investigations discussing porous media are referenced in [25–28], among many others.
within Darcian velocity. This became known as the Forchheimer term, as designated by Muskat [19]. Nasir et al [20] scrutinized the radiative 3D Darcy-Forchheimer flow of carbon nanotubes past a stretchable rotating disk. They posited that fluid velocity falls with an upsurge in inertia and porosity parameters. Jha and Kaurangini [21] presented analytic solutions for Darcy-Forchheimer-based spongy media relations. Kaladhar [22] discussed mixed convection flow with dual stratification effects within a Darcy-Forchheimer medium, finding that velocity is reduced for higher estimates of Darcy-Forchheimer number. A numerical solution for a second law analysis of ferrofluid within a spongy semi annulus is investigated by Sheikholeslami et al [23]. Alamri et al [24] proposed the model of a radiative plane Poiseuille flow of nanofluid, using slip conditions past a porous medium. Some recent investigations discussing porous media are referenced in [25–28], among many others.
Based on the above discussion, it can be noted that there is as yet no study in which the influences of Cattaneo-Christov heat flux with carbon nanotubes in a Darcy-Forchheimer porous media are examined between two parallel disks. Comparatively little research has been conducted in the area of carbon nanotubes to date. For this reason, this paper aims to examine melting heat transfer effects in carbon nanotubes- (SWCNTs and MWCNTs) based nanofluid unsteady flow, in a non-linear Darcy-Forchheimer permeable media, between two parallel disks, with Cattaneo-Christov heat flux and homogeneous–heterogeneous reactions. The impact of prominent parameters on surface drag force, and Nusselt number, are portrayed via graphic illustrations. The numerical solution of the present work is obtained by adopting the Finite difference method, this being the default in the bvp4c built-in function of the MATLAB scheme. The layout of this paper consists of: Section one – introduction. Section two is devoted to mathematical modeling, with all required equations, having employed the boundary layer theory to partial differential equations. Section three is a detailed elaboration of the numerical methods applied to the problem. Section four covers results and discussion. The paper concludes with Final remarks and summing up.
Mathematical modeling
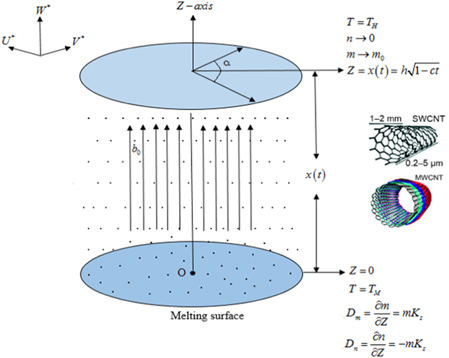
Consider an incompressible, time-dependent 2D MHD nanofluid flow, containing CNTs within a Darcy-Forchheimer spongy media under conditions of non-linear thermal radiation and melting heat transfer, between two infinite parallel disks of length
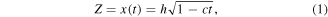
with applied magnetic strength  which is normal to the disks (figure 1). Here, SWCNTs and MWCNTs, along with water (base fluid), are considered. Moreover, the upper disk
which is normal to the disks (figure 1). Here, SWCNTs and MWCNTs, along with water (base fluid), are considered. Moreover, the upper disk  moves up and down with a velocity
moves up and down with a velocity  from the fixed and porous lower disk
from the fixed and porous lower disk  The induced magnetic field is neglected here, because we are using a small Reynolds number. We also consider the cylindrical coordinate system
The induced magnetic field is neglected here, because we are using a small Reynolds number. We also consider the cylindrical coordinate system  The velocity component
The velocity component  vanishes identically due to rotational flow symmetry
vanishes identically due to rotational flow symmetry 
Figure 1. Fluid geometry.
Download figure:
Standard image High-resolution imageWe assume a model, designed by Chaudhary and Merkin [29] for homogeneous–heterogeneous chemical reactions defined as:
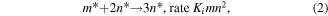
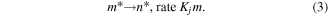
These reactions are presumed to be isothermal. The governing system with boundary layer equations are represented as:

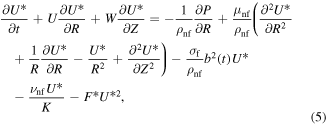
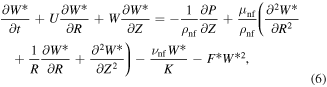
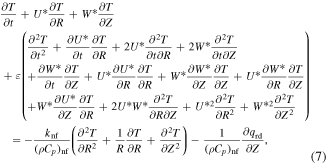
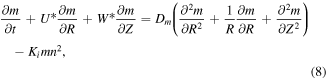
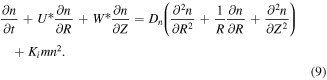
With boundary conditions
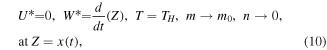
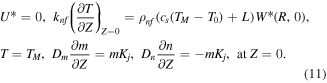
Mathematically, thermophysical properties are shown as:
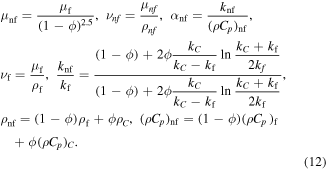
The thermophysical features of water and CNTs are appended in table 1.
Table 1. Thermophysical characteristics of base fluid, SWCNTs and MWCNTs [30].
| Thermophysical traits |
|
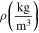
|
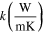
|
|---|---|---|---|
| Water (base fluid) | 4179.00 | 997.100 | 0.613 00 |
| Nanoparticles (SWCNTs) | 425 | 2600 | 6600 |
| Nanoparticles (MWCNTs) | 796 | 1600 | 3000 |
From equation (7), by utilizing the Roseland thermal radiation approximation [31], we obtain the value of  as:
as:
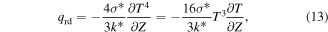
with
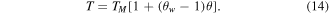
Similarity transformation
Similarity transformations are defined as:
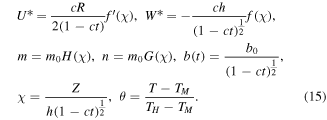
By means of the above transformation, equation (4) is satisfied, and equations (5)–(9) are transformed into:
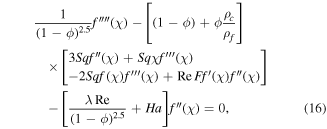
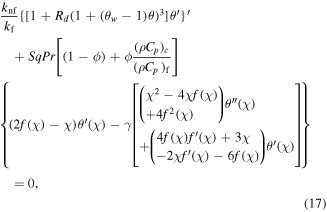
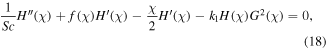
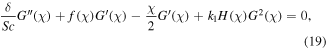
with
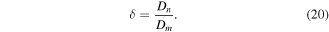
Based on equations (2) and (3), chemical species  and
and  cannot be analogous, but both can be identical in magnitude, provided
cannot be analogous, but both can be identical in magnitude, provided  Thus, from equation (20), presuming that
Thus, from equation (20), presuming that  and
and  are identical (i.e.,
are identical (i.e.,  ), we obtain
), we obtain

using the above property, equations (18) and (19) become
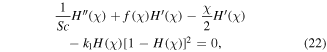
and the boundary Equations (10) and (11) become
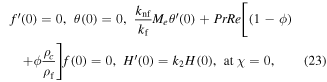
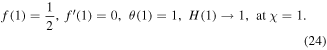
Based on equation (23),  is the melting heat coefficient as:
is the melting heat coefficient as:
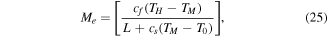
which is the amalgamation of two numbers,  , and
, and  , known as Stefan numbers, for solid and liquid states. In the above equations, non-dimensional coefficients are defined as:
, known as Stefan numbers, for solid and liquid states. In the above equations, non-dimensional coefficients are defined as:
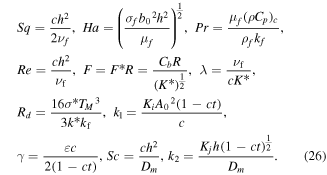
Surface drag force and rate of heat flux are classified by:
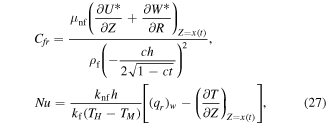
using equation (15), we get
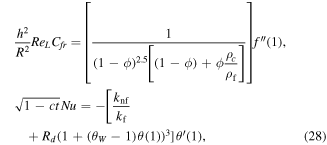
where
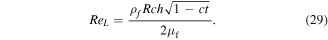
Solution methodology
For non-linear systems of ODEs (16), (17), and (22), with boundary conditions (23) and (24), we employ the finite difference default method of the bvp4c built-in function of the MATLAB scheme, which is fourth order accurate, and a grid size of 0.01 is taken with the tolerance  Using the following numerical code, we obtain first order ODEs as:
Using the following numerical code, we obtain first order ODEs as:
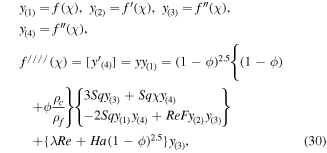
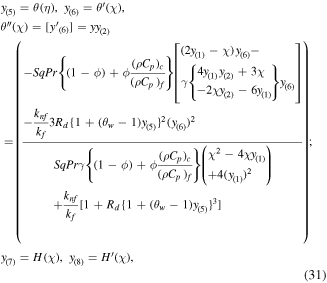
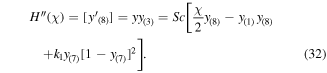
With the boundary conditions
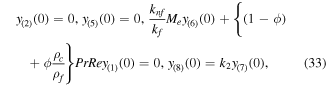
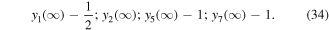
Results and discussion
This segment examines the outcomes of dimensionless velocity  temperature
temperature  , and concentration fields
, and concentration fields  for numerous arising parameters, so as to reflect the behavior of fluid flow, and heat and mass transport. The subsequent discussion is presented for both SWCNTs and MWCNTs. Parameters used in this analysis are
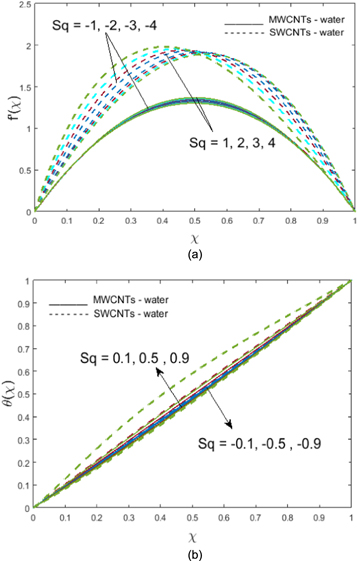
for numerous arising parameters, so as to reflect the behavior of fluid flow, and heat and mass transport. The subsequent discussion is presented for both SWCNTs and MWCNTs. Parameters used in this analysis are  Figure 2(a) illustrates how positive and negative values of squeezed number
Figure 2(a) illustrates how positive and negative values of squeezed number  affect velocity
affect velocity  The graph illustrates how, for both single and multi-walled CNTs, velocity profile
The graph illustrates how, for both single and multi-walled CNTs, velocity profile  increases with the contraction of disks, i.e., negative values, whereas for positive values where upper and lower plates are driven further apart, the opposite behavior can be observed. In the case of contraction
increases with the contraction of disks, i.e., negative values, whereas for positive values where upper and lower plates are driven further apart, the opposite behavior can be observed. In the case of contraction  the fluid is exposed to a squeezed force, which causes it to move with increased velocity. Hence, velocity is augmented. Nevertheless, for
the fluid is exposed to a squeezed force, which causes it to move with increased velocity. Hence, velocity is augmented. Nevertheless, for  when both disks move away from each other, a gap is produced between the disks. The fluid moves in a reverse direction to fill this gap; thus, velocity reduces. In figure 2(b) effect of the
when both disks move away from each other, a gap is produced between the disks. The fluid moves in a reverse direction to fill this gap; thus, velocity reduces. In figure 2(b) effect of the  squeezing parameter is exhibited versus
squeezing parameter is exhibited versus  In the case of the contraction of disks
In the case of the contraction of disks  the temperature profile
the temperature profile  establishes diminishing behavior, whereas an opposite trend is seen when the disks are driven apart from each other i.e.
establishes diminishing behavior, whereas an opposite trend is seen when the disks are driven apart from each other i.e.  This is because movement of fluid increases when disks are driving away from each other, thus the temperature increases. An inverse impact of the melting heat transfer parameter
This is because movement of fluid increases when disks are driving away from each other, thus the temperature increases. An inverse impact of the melting heat transfer parameter  can be observed in figures 3(a) and (b), for velocity
can be observed in figures 3(a) and (b), for velocity  and temperature
and temperature  profiles, respectively. As the molecular motion enhances due to melting heat transit, owing to the fact that
profiles, respectively. As the molecular motion enhances due to melting heat transit, owing to the fact that  leads to increased molecular motion from hot fluid toward cold surface, which in turn causes an increase in velocity. In contrast, with the temperature field, convective flow causes heat transfer to the melting surface more promptly, which results in decreasing temperature
leads to increased molecular motion from hot fluid toward cold surface, which in turn causes an increase in velocity. In contrast, with the temperature field, convective flow causes heat transfer to the melting surface more promptly, which results in decreasing temperature  Figures 4(a) and (b) depict the effect of the local inertia coefficient
Figures 4(a) and (b) depict the effect of the local inertia coefficient  on velocity
on velocity  and temperature
and temperature  of fluid flow. It can be observed that local inertia coefficient
of fluid flow. It can be observed that local inertia coefficient  has an inverse influence on both fields. Here, velocity falls whereas temperature increases. As porous media cause resistance in a fluid flow, the result is a reduction in dimensionless velocity
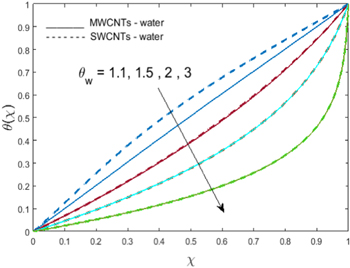
has an inverse influence on both fields. Here, velocity falls whereas temperature increases. As porous media cause resistance in a fluid flow, the result is a reduction in dimensionless velocity  Figure 5 illustrates the behavior of the temperature ratio parameter
Figure 5 illustrates the behavior of the temperature ratio parameter  on fluid temperature. A retarding effect of
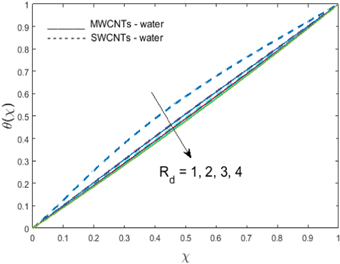
on fluid temperature. A retarding effect of  on dimensionless temperature can be observed. The effects of porosity parameter
on dimensionless temperature can be observed. The effects of porosity parameter  on radial velocity are shown in figure 6, where velocity falls for higher values of
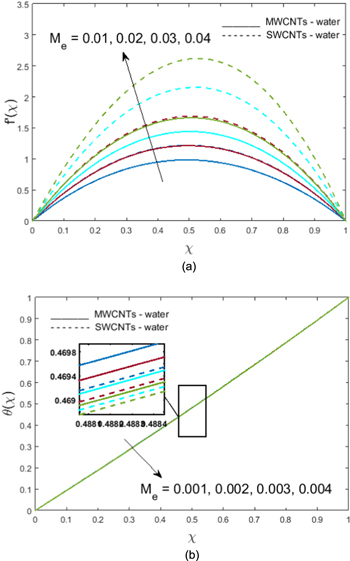
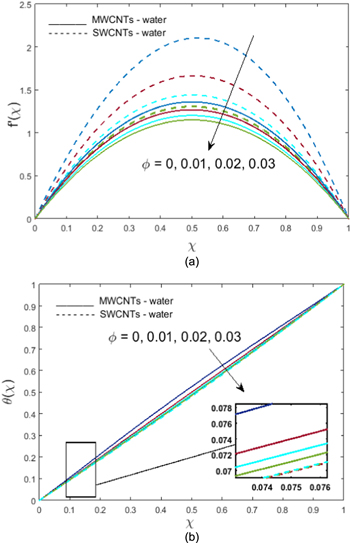
on radial velocity are shown in figure 6, where velocity falls for higher values of  The porosity of spongy media causes high resistivity to fluid flow; hence, velocity declines. Figures 7(a) and (b) show the impact of the nanoparticle volume fraction parameter
The porosity of spongy media causes high resistivity to fluid flow; hence, velocity declines. Figures 7(a) and (b) show the impact of the nanoparticle volume fraction parameter  on the radial velocity
on the radial velocity  , and temperature
, and temperature  of the fluid. An increase in the quantity of nanoparticles in the base fluid (water) leads to a thickening of the fluid. Due to this, velocity reduces (figure 7(a)). On the other hand, in figure 7(b), for ordinary fluid (i.e.,
of the fluid. An increase in the quantity of nanoparticles in the base fluid (water) leads to a thickening of the fluid. Due to this, velocity reduces (figure 7(a)). On the other hand, in figure 7(b), for ordinary fluid (i.e.,  in the absence of volume proportion) the temperature field is highest when the disks are driven further from each other (i.e.,
in the absence of volume proportion) the temperature field is highest when the disks are driven further from each other (i.e.,  ), while augmentation of volume fraction
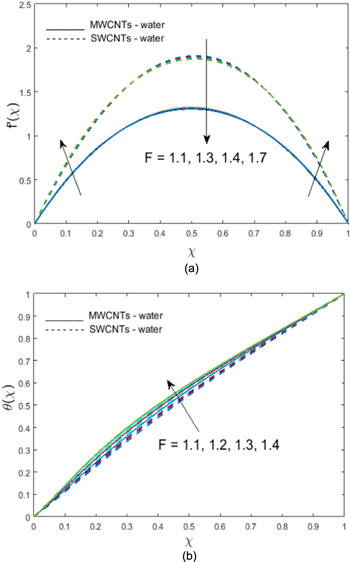
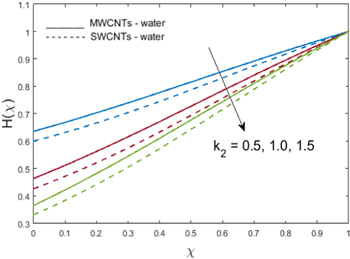
), while augmentation of volume fraction  causes a reduction in the temperature of the fluid. This is because the thermal conductivity of nanofluid increases by using a small concentration of nanoparticles, and when we increase the volume of nanoparticles, the thermal conductivity of the nanofluid decreases; hence, the temperature decreases. Figure 8 demonstrates the effects of the radiation parameter
causes a reduction in the temperature of the fluid. This is because the thermal conductivity of nanofluid increases by using a small concentration of nanoparticles, and when we increase the volume of nanoparticles, the thermal conductivity of the nanofluid decreases; hence, the temperature decreases. Figure 8 demonstrates the effects of the radiation parameter  on the temperature
on the temperature  The temperature drops for larger values of
The temperature drops for larger values of  The transfer of energy to the fluid declines owing to higher estimates of
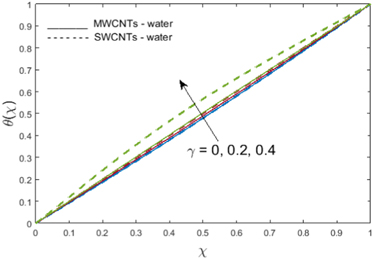
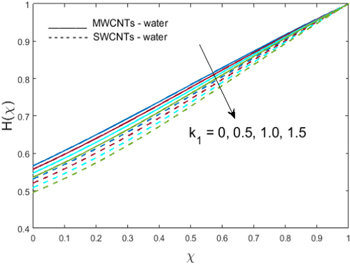
The transfer of energy to the fluid declines owing to higher estimates of  thus decreasing the fluid temperature. In figure 9, the impact of the thermal relaxation time coefficient
thus decreasing the fluid temperature. In figure 9, the impact of the thermal relaxation time coefficient  is shown. Higher values of
is shown. Higher values of  cause an increment in dimensionless temperature
cause an increment in dimensionless temperature  for both types of CNTs. Figure 10 indicates that concentration
for both types of CNTs. Figure 10 indicates that concentration  decreases for higher values of
decreases for higher values of  The same outcome can be detected in figure 11 for
The same outcome can be detected in figure 11 for  It is therefore deduced that concentration eventually reduces as the reactants are used throughout homogeneous–heterogeneous reactions. The effects of Schmidt number
It is therefore deduced that concentration eventually reduces as the reactants are used throughout homogeneous–heterogeneous reactions. The effects of Schmidt number  are portrayed in figure 12. The concentration profile is reduced for increasing values of
are portrayed in figure 12. The concentration profile is reduced for increasing values of  As
As  is the ratio of momentum to mass diffusivity, greater
is the ratio of momentum to mass diffusivity, greater  estimates indicate lower mass diffusivity, which causes a reduction in fluid concentration
estimates indicate lower mass diffusivity, which causes a reduction in fluid concentration  In figure 13, a retardation effect of porosity parameter
In figure 13, a retardation effect of porosity parameter  on local inertia coefficient
on local inertia coefficient  can be observed for surface drag force. Influences of melting parameter
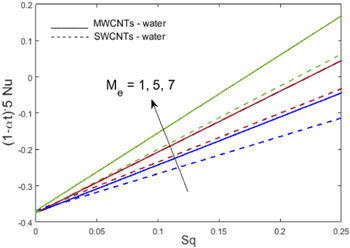
can be observed for surface drag force. Influences of melting parameter  and squeezing parameter
and squeezing parameter  on the rate of heat transfer are depicted in figure 14. Here, it can be observed that augmentation in the melting coefficient
on the rate of heat transfer are depicted in figure 14. Here, it can be observed that augmentation in the melting coefficient  causes an increment in the rate of heat transfer. Since molecular motion increases with high melting heat transmission, hence the rate of heat is increased when we augment the melting parameter. Figure 15 illustrates the impact of radiation coefficient
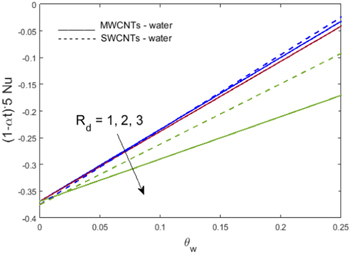
causes an increment in the rate of heat transfer. Since molecular motion increases with high melting heat transmission, hence the rate of heat is increased when we augment the melting parameter. Figure 15 illustrates the impact of radiation coefficient  and temperature ratio coefficient
and temperature ratio coefficient  on the Nusselt number. The rate of heat transfer falls for larger estimates of
on the Nusselt number. The rate of heat transfer falls for larger estimates of  This is because the energy from radiation phenomena is being used in the melting .process; thus, a significant decay in the Nusselt number can be seen.
This is because the energy from radiation phenomena is being used in the melting .process; thus, a significant decay in the Nusselt number can be seen.
Figure 2. (a). Variations of squeezing parameter  on radial velocity
on radial velocity  (b). Variations of squeezing parameter
(b). Variations of squeezing parameter  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 3. (a). Variations of melting parameter  on radial velocity
on radial velocity  (b). Variations of melting parameter
(b). Variations of melting parameter  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 4. (a). Variations of local inertia coefficient  on radial velocity
on radial velocity  (b). Variations of local inertia coefficient
(b). Variations of local inertia coefficient  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 5. Variations of temperature ratio parameter  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 6. Variations of porosity parameter  on radial velocity
on radial velocity 
Download figure:
Standard image High-resolution imageFigure 7. (a). Variations of nanoparticle volume fraction  on radial velocity
on radial velocity  (b). Variations of nanoparticle volume fraction
(b). Variations of nanoparticle volume fraction  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 8. Variations of radiation coefficient  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 9. Variations of thermal relaxation parameter  on temperature distribution
on temperature distribution 
Download figure:
Standard image High-resolution imageFigure 10. Variations of homogeneous reaction Coefficient  on concentration distribution
on concentration distribution 
Download figure:
Standard image High-resolution imageFigure 11. Variations of heterogeneous reaction coefficient  on concentration distribution
on concentration distribution 
Download figure:
Standard image High-resolution imageFigure 12. Variations of Schmidt number  on concentration distribution
on concentration distribution 
Download figure:
Standard image High-resolution imageFigure 13. Variations of porosity parameter  and local inertia parameter
and local inertia parameter  on surface drag force.
on surface drag force.
Download figure:
Standard image High-resolution imageFigure 14. Variations of melting parameter  and squeezing parameter
and squeezing parameter  on Nusselt number.
on Nusselt number.
Download figure:
Standard image High-resolution imageFigure 15. Variations of radiation parameter  and temperature ratio parameter
and temperature ratio parameter  on Nusselt number.
on Nusselt number.
Download figure:
Standard image High-resolution imageTable 2 depicts the comparative estimates of surface drag force for various values of squeezing parameter and Hartmann number, with Lu et al [15] as limiting case. A remarkable resemblance is achieved in this regard.
Table 2. Comparative results of surface drag force for distinct values of squeezing parameter and Hartmann number with Lu et al [15].
|
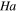
|
Lu et al [15] | Present results |
|---|---|---|---|
| 0.5 | 0.0 | −3.146 1941 | −3.134 6178 |
| 1.0 | −3.194 0816 | −3.183 3610 | |
| 2.0 | −3.241 3602 | −3.236 7145 | |
| −1.0 | 1.0 | −2.759 6174 | −2.747 1465 |
| 0.0 | −3.049 6468 | −3.031 1268 | |
| 1.0 | −3.338 1297 | −3.327 8263 |
Concluding remarks
In the presented model, 2D time-dependent magnetohydrodynamic squeezing nanofluid flow between two parallel disks with suspended carbon nanotubes is discussed. The analysis is performed under conditions of non-linear thermal radiation, amalgamated with melting heat, and homogeneous–heterogeneous reactions. Cattaneo-Christov heat flux is engaged in place of the conventional Fourier law of heat conduction. The proposed model is transformed into a non-linear form and processed by means of the default Finite difference method of the bvp4c built-in function of the MATLAB scheme. The key findings of the presented model are:
- The local inertia coefficient has an opposite impact on the radial velocity and temperature field.
- Porous media creates resistance in a fluid flow, resulting in a reduction in fluid velocity and an augmentation in the temperature of the fluid.
- The melting parameter has a retarding effect on temperature, whereas radial velocity increases.
- An increase in the radiation coefficient leads to a reduction in the temperature of the fluid.
- Radiative energy is being used in the melting process; consequently, the temperature of the fluid decreases.
- The porosity coefficient has a retarding influence on radial velocity and surface drag force.
Acknowledgments
This work is supported by Bahria University, Islamabad, Pakistan.
Competing interests statement
Authors have no conflict of interest regarding this publication.