Skip to main content
Springer Nature Link
Log in

A Novel Unstructured Mesh Finite Element Method for Solving the Time-Space Fractional Wave Equation on a Two-Dimensional Irregular Convex Domain

  • Research Paper
  • Published:
Fractional Calculus and Applied Analysis Aims and scope Submit manuscript

Abstract

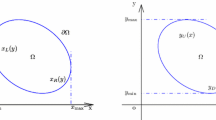
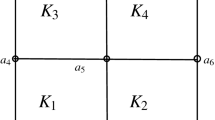
Most existing research on applying the finite element method to discretize space fractional operators is studied on regular domains using either uniform structured triangular meshes, or quadrilateral meshes. Since many practical problems involve irregular convex domains, such as the human brain or heart, which are difficult to partition well with a structured mesh, the existing finite element method using the structured mesh is less efficient. Research on the finite element method using a completely unstructured mesh on an irregular domain is of great significance. In this paper, a novel unstructured mesh finite element method is developed for solving the time-space fractional wave equation on a two-dimensional irregular convex domain. The novel unstructured mesh Galerkin finite element method is used to discretize in space and the Crank-Nicholson scheme is used to discretize the Caputo time fractional derivative. The implementation of the unstructured mesh Crank-Nicholson Galerkin method (CNGM) is detailed and the stability and convergence of the numerical scheme are analyzed. Numerical examples are presented to verify the theoretical analysis. To highlight the ability of the proposed unstructured mesh Galerkin finite element method, a comparison of the unstructured mesh with the structured mesh in the implementation of the numerical scheme is conducted. The proposed numerical method using an unstructured mesh is shown to be more effective and feasible for practical applications involving irregular convex domains.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. E. Bazhlekova, I. Bazhlekov, Viscoelastic flows with fractional derivative models: Computational approach by convolutional calculus of Dimovski. Fract. Calc. Appl. Anal. 17, No 4 (2014), 954–976; 10.2478/s13540-014-0209-x; https://www.degruyter.com/view/j7fca.2014.17.issue-4/issue-files/fca.2014.17.issue-4.xml.

    Article  MathSciNet  Google Scholar 

  2. W. Bu, X. Liu, Y. Tang, J. Yang, Finite element multigrid method for multi-term time fractional advection diffusion equations. Int. J. Model. Simul. Sci. Comput. 6, No 1 (2015), ID # 1540001.

    Google Scholar 

  3. W. Bu, Y. Tang, Y. Wu, J. Yang, Finite difference/finite element method for two-dimensional space and time fractional Bloch-Torrey equations. J. Comput. Phys. 293 (2015), 264–279.

    Article  MathSciNet  Google Scholar 

  4. W. Bu, Y. Tang, J. Yang, Galerkin finite element method for twodimensional Riesz space fractional diffusion equations. J. Comput. Phys. 276 (2014), 26–38.

    Article  MathSciNet  Google Scholar 

  5. S. Chen, F. Liu, X. Jiang, I. Turner, K. Burrage, Fast finite difference approximation for identifying parameters in a two-dimensional space-fractional nonlocal model with variable diffusivit coefficients. SIAM J. Numer. Anal. 54, No 2 (2016), 606–624.

    Article  MathSciNet  Google Scholar 

  6. Y.J. Choi, S.K. Chung, Finite element solutions for the space fractional diffusion equation with a nonlinear source term. In Abstr. Appl. Anal. 2012 (2012) Article # 596184, 25 pp.

  7. G.R. Cowper, Gaussian quadrature formulas for triangles. Int. J. Numer. Meth. Eng. 7, No 3 (1973), 405–408.

    Article  Google Scholar 

  8. M. Cristescu, G. Loubignac, Gaussian Quadrature Formulas for Functions with Singularities in 1/R over Triangles and Quadrangles. Pentech Press, London (1978).

    MATH  Google Scholar 

  9. V.J. Ervin, J.P. Roop, Variational formulation for the stationary fractional advection dispersion equation. Numer. Meth. Part. D. E. 22, No 3 (2006), 558–576.

    Article  MathSciNet  Google Scholar 

  10. V.J. Ervin, J.P. Roop, Variational solution of fractional advection dispersion equations on bounded domains in Rd. Numer. Meth. Part. D. E. 23 (2007), 256–281.

    Article  Google Scholar 

  11. W. Fan, X. Jiang, S. Chen, Parameter estimation for the fractional fractal diffusion model based on its numerical solution. Comput. Math. Appl. 71, No 2 (2016), 642–651.

    Article  MathSciNet  Google Scholar 

  12. L. Feng, P. Zhuang, F. Liu, I. Turner, Stability and convergence of a new finite volume method for a two-sided space-fractional diffusion equation. Appl. Math. Comput. 257 (2015), 52–65.

    MathSciNet  MATH  Google Scholar 

  13. N. Ford, J. Xiao, Y. Yan, A finite element method for time fractional partial differential equations. Fract. Calc. Appl. Anal. 14, No 3 (2011), 454–474; 10.2478/s13540-011-0028-2; https://www.degruyter.eom/view/j/fca.2011.14.issue-3/issue-files/fca.2011.14.issue-3.xml.

    Article  MathSciNet  Google Scholar 

  14. C. Geuzaine J. F. Remacle, Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Meth. Eng. 79, No 11 (2009), 1309–1331.

    Article  MathSciNet  Google Scholar 

  15. C. Gong, W. Bao, G. Tang, A parallel algorithm for the Riesz fractional reaction-diffusion equation with explicit finite difference method. Fract. Calc. Appl. Anal. 16, No 3 (2013), 654–669; 10.2478/s13540-013-0041-8; https://www.degruyter.com/view/j/fca.2013.16.issue-3/issue-files/fca.2013.16.issue-3.xml.

    Article  MathSciNet  Google Scholar 

  16. H. Hejazi, T. Moroney, F. Liu, Stability and convergence of a finite volume method for the space fractional advection-dispersion equation. J. Comput. Appl. Math. 255 (2014), 684–697.

    Article  MathSciNet  Google Scholar 

  17. R. Hilfer, Applications of Fractional Calculus in Physics. World Scientific (2000).

    MATH  Google Scholar 

  18. X. Jiang, H. Qi, Thermal wave model of bioheat transfer with modified Riemann-Liouville fractional derivative. J. Phys. A: Math. Theor. 45, No 48 (2012), ID # 485101, 11 pp.

    Google Scholar 

  19. C. Li, Z. Zhao, Y. Chen, Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion. Comput. Math. Appl. 62 No 3 (2011), 855–875.

    Article  MathSciNet  Google Scholar 

  20. F. Liu, P. Zhuang, Q. Liu, Numerical Methods of Fractional Partial Differential Equations and Applications. Science Press, Beijing (2015) (In Chinese).

    Google Scholar 

  21. L. Liu, L. Zheng, F. Liu, X. Zhang, Anomalous convection diffusion and wave coupling transport of cells on comb frame with fractional Cattaneo-Christov flux. Commun. Nonlinear Sci. 38 (2016), 45–58.

    Article  MathSciNet  Google Scholar 

  22. I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications. Academic Press (1998).

    MATH  Google Scholar 

  23. J.P. Roop, Variational solution of the fractional advection dispersion equation. Ph.D. Thesis (2004).

    Google Scholar 

  24. Z. Sun, X. Wu, A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56, No 2 (2006), 193–209.

    Article  MathSciNet  Google Scholar 

  25. B. Yu, X. Jiang, H. Xu, A novel compact numerical method for solving the two-dimensional non-linear fractional reaction-subdiffusion equation. Numer. Algorithms 68, No 4 (2015), 923–950.

    Article  MathSciNet  Google Scholar 

  26. F. Zeng, F. Liu, C. Li, K. Burrage, I. Turner, V. Anh, A Crank- Nicolson ADI spectral method for a two-dimensional Riesz space fractional nonlinear reaction-diffusion equation. SIAM J. Numer. Anal. 52, No 6 (2014), 2599–2622.

    Article  MathSciNet  Google Scholar 

  27. H. Zhang, F. Liu, V. Anh, Galerkin finite element approximation of symmetric space-fractional partial differential equations. Appl. Math. Comput. 217, No 6 (2010), 2534–2545.

    MathSciNet  MATH  Google Scholar 

  28. Y. Zhao, W. Bu, J. Huang, D. Liu, Y. Tang, Finite element method for two-dimensional space-fractional advection-dispersion equations. App. Math. Comput. 257 (2015), 553–565.

    Article  MathSciNet  Google Scholar 

  29. Y. Zhao, Y. Zhang, D. Shi, F. Liu, I. Turner, Superconvergence analysis of nonconforming finite element method for two-dimensional time fractional diffusion equations. Appl. Math. Lett. 59 (2016), 38–47.

    Article  MathSciNet  Google Scholar 

  30. M. Zheng, F. Liu, V. Anh, I. Turner, A high-order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 40, No 7 (2016), 4970–4985.

    Article  MathSciNet  Google Scholar 

  31. X. Zhu, Y. Nie, J. Wang, Z. Yuan, A numerical approach for the Riesz space-fractional Fisher’ equation in two-dimensions. Int. J. Comput. Math. (2015), 1–20.

    Google Scholar 

  32. P. Zhuang, F. Liu, I. Turner, Y. Gu, Finite volume and finite element methods for solving a one-dimensional space-fractional Boussinesq equation. Appl. Math. Model. 38, No 15 (2014), 3860–3870.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University Jinan, 250100, PR China

    Wenping Fan

  2. School of Mathematical Sciences, Queensland University of Technology GPO, Box 2434, Brisbane, QLD 4001, Australia

    Fawang Liu

  3. School of Mathematics, Shandong University, Jinan, 250100, PR China

    Xiaoyun Jiang

  4. Australian Research Council Centre of Excellence for Mathematics and Statistical Frontiers School of Mathematical Sciences, Queensland University of Technology GPO, Box 2434, Brisbane, QLD 4001, Australia

    Ian Turner

Authors
  1. Wenping Fan
    View author publications

    Search author on:PubMed Google Scholar

  2. Fawang Liu
    View author publications

    Search author on:PubMed Google Scholar

  3. Xiaoyun Jiang
    View author publications

    Search author on:PubMed Google Scholar

  4. Ian Turner
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Wenping Fan.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fan, W., Liu, F., Jiang, X. et al. A Novel Unstructured Mesh Finite Element Method for Solving the Time-Space Fractional Wave Equation on a Two-Dimensional Irregular Convex Domain. FCAA 20, 352–383 (2017). https://doi.org/10.1515/fca-2017-0019

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1515/fca-2017-0019

Keywords

Keywords