Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Non-Abelian braiding on photonic chips

Nature Photonics volume 16, pages 390–395 (2022)Cite this article

Subjects

Abstract

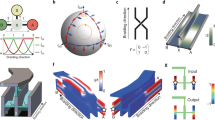
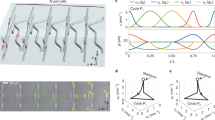
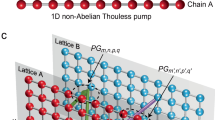
Non-Abelian braiding has attracted substantial attention because of its pivotal role in describing the exchange behaviour of anyons—candidates for realizing quantum logics. The input and outcome of non-Abelian braiding are connected by a unitary matrix that can also physically emerge as a geometric-phase matrix in classical systems. Hence it is predicted that non-Abelian braiding should have analogues in photonics, although a feasible platform and the experimental realization remain out of reach. Here we propose and experimentally realize an on-chip photonic system that achieves the non-Abelian braiding of up to five photonic modes. The braiding is realized by controlling the multi-mode geometric-phase matrix in judiciously designed photonic waveguide arrays. The quintessential effect of braiding—sequence-dependent swapping of photon dwell sites—is observed in both classical-light and single-photon experiments. Our photonic chips are a versatile and expandable platform for studying non-Abelian physics, and we expect the results to motivate next-generation non-Abelian photonic devices.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Two-mode braiding in photonic waveguides.
Fig. 2: Measurement of the geometric phase in two-mode braiding.
Fig. 3: Non-Abelian braiding of three modes.
Fig. 4: Multi-mode braiding.

Similar content being viewed by others

Data availability

The data that support the findings of this work are available from the corresponding authors upon reasonable request.

Code availability

The codes used for performing the theoretical analysis and numerical simulations are available from X.-L.Z. upon reasonable request.

References

  1. Leinaas, J. & Myrheim, J. On the theory of identical particles. Nuovo Cimento B 37, 1–23 (1977).

    Article  ADS  Google Scholar 

  2. Wilczek, F. Magnetic flux, angular momentum, and statistics. Phys. Rev. Lett. 48, 1144–1146 (1982).

    Article  ADS  Google Scholar 

  3. Wilczek, F. Quantum mechanics of fractional-spin particles. Phys. Rev. Lett. 49, 957–959 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  4. Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  5. Wilczek, F. Fractional Statistics and Anyon Superconductivity (World Scientific, 1990).

  6. Fredenhagen, K., Rehren, K. H. & Schroer, B. Superselection sectors with braid group statistics and exchange algebras. Commun. Math. Phys. 125, 201–226 (1989).

    Article  ADS  MathSciNet  Google Scholar 

  7. Lutchyn, R. M. et al. Majorana zero modes in superconductor-semiconductor heterostructures. Nat. Rev. Mater. 3, 52–68 (2018).

    Article  ADS  Google Scholar 

  8. Wang, D. et al. Evidence for Majorana bound states in an iron-based superconductor. Science 362, 333–335 (2018).

    Article  ADS  Google Scholar 

  9. Huang, H. L. et al. Emulating quantum teleportation of a Majorana zero mode qubit. Phys. Rev. Lett. 126, 090502 (2021).

    Article  ADS  Google Scholar 

  10. Willett, R. L., Nayak, C., Shtengel, K., Pfeiffer, L. N. & West, K. W. Magnetic-field-tuned Aharonov–Bohm oscillations and evidence for non-Abelian anyons at ν = 5/2. Phys. Rev. Lett. 111, 186401 (2013).

    Article  ADS  Google Scholar 

  11. Bartolomei, H. et al. Fractional statistics in anyon collisions. Science 368, 173–177 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  12. Nakamura, J., Liang, S., Gardner, M. C. & Manfra, M. J. Direct observation of anionic braiding statistics. Nat. Phys. 16, 931–936 (2020).

    Article  Google Scholar 

  13. Zu, C. et al. Experimental realization of universal geometric quantum gates with solid-state spins. Nature 514, 72–75 (2014).

    Article  ADS  Google Scholar 

  14. Chen, Z. G., Zhang, R. Y., Chan, C. T. & Ma, G. Classical non-Abelian braiding of acoustic modes. Nat. Phys. 18, 179–184 (2022).

    Article  Google Scholar 

  15. Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indiana Acad. Sci. A44, 247–262 (1956).

    MathSciNet  Google Scholar 

  16. Zhuo, W., Sun, S., He, Q. & Zhou, L. A review of high-efficiency Pancharatnam–Berry metasurfaces. Terahertz Sci. Technol. 13, 73–89 (2020).

    Article  Google Scholar 

  17. Dalibard, J., Gerbier, F., Juzeliunas, G. & Öhberg, P. Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011).

    Article  ADS  Google Scholar 

  18. Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  19. Umucalilar, R. O. & Carusotto, I. Many-body braiding phases in a rotating strongly correlated photon gas. Phys. Lett. A 377, 2074–2078 (2013).

    Article  ADS  MathSciNet  Google Scholar 

  20. Iadecola, T., Schuster, T. & Chamon, C. Non-Abelian braiding of light. Phys. Rev. Lett. 117, 073901 (2016).

    Article  ADS  Google Scholar 

  21. Dutta, S. & Mueller, E. J. Coherent generation of photonic fractional quantum Hall states in a cavity and the search for anyonic quasiparticles. Phys. Rev. A 97, 033825 (2018).

    Article  ADS  Google Scholar 

  22. Boross, P., Asbóth, J. K., Széchenyi, G., Oroszlány, L. & Pályi, A. Poor man’s topological quantum gate based on the Su-Schrieffer-Heeger model. Phys. Rev. B 100, 045414 (2019).

    Article  ADS  Google Scholar 

  23. Kremer, M., Teuber, L., Szameit, A. & Scheel, S. Optimal design strategy for non-Abelian geometric phases using Abelian gauge fields based on quantum metric. Phys. Rev. Res. 1, 033117 (2019).

    Article  Google Scholar 

  24. Chen, Y. et al. Non-Abelian gauge field optics. Nat. Commun. 10, 3125 (2019).

    Article  ADS  Google Scholar 

  25. Yang, Y. et al. Synthesis and observation of non-Abelian gauge fields in real space. Science 365, 1021–1025 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  26. Guo, Q. et al. Experimental observation of non-Abelian topological charges and edge states. Nature 594, 195–200 (2021).

    Article  ADS  Google Scholar 

  27. Xu, J. S. et al. Simulating the exchange of Majorana zero modes with a photonic system. Nat. Commun. 7, 13194 (2016).

    Article  ADS  Google Scholar 

  28. Xu, J. S. et al. Photonic implementation of Majorana-based Berry phases. Sci. Adv. 4, eaat6533 (2018).

    Article  ADS  Google Scholar 

  29. Ma, L. B. et al. Spin–orbit coupling of light in asymmetric microcavities. Nat. Commun. 7, 10983 (2016).

    Article  ADS  Google Scholar 

  30. Yang, Y., Zhen, B., Joannopoulos, J. D. & Soljačić, M. Non-Abelian generalizations of the Hofstadter model: spin–orbit-coupled butterfly pairs. Light Sci. Appl. 9, 177 (2020).

    Article  ADS  Google Scholar 

  31. Brosco, V., Pilozzi, L., Fazio, R. & Conti, C. Non-Abelian Thouless pumping in a photonic lattice. Phys. Rev. A 103, 063518 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  32. Wang, D. et al. Intrinsic in-plane nodal chain and generalized quaternion charge protected nodal link in photonics. Light Sci. Appl. 10, 83 (2021).

    Article  ADS  Google Scholar 

  33. Noh, J. et al. Braiding photonic topological zero modes. Nat. Phys. 16, 989–993 (2020).

    Article  Google Scholar 

  34. Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).

    Article  ADS  Google Scholar 

  35. Klauck, F. et al. Observation of PT-symmetric quantum interference. Nat. Photon. 13, 883–887 (2019).

    Article  ADS  Google Scholar 

  36. Davis, K. M., Miura, K., Sugimoto, N. & Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 21, 1729–1731 (1996).

    Article  ADS  Google Scholar 

  37. Yu, F., Zhang, X. L., Tian, Z. N., Chen, Q. D. & Sun, H. B. General rules governing the dynamical encircling of an arbitrary number of exceptional points. Phys. Rev. Lett. 127, 253901 (2021).

    Article  ADS  Google Scholar 

  38. Barenco, A., Deutsch, D., Ekert, A. & Jozsa, R. Conditional quantum dynamics and logic gates. Phys. Rev. Lett. 74, 4083–4086 (1995).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11922416, 11974140, 61825502, 61827826 and 61960206003), China Postdoctoral Science Foundation (2019T120234) and the Hong Kong Research Grants Council (12302420, 12300419, 22302718 and C6013-18G). X.-L.Z. and G.M. thank C. T. Chan and R.-Y. Zhang for fruitful discussions.

Author information

Author notes

  1. These authors contributed equally: Xu-Lin Zhang, Feng Yu.

Authors and Affiliations

  1. State Key Laboratory of Integrated Optoelectronics, College of Electronic Science and Engineering, Jilin University, Changchun, China

    Xu-Lin Zhang, Feng Yu, Zhen-Nan Tian, Qi-Dai Chen & Hong-Bo Sun

  2. Department of Physics, Hong Kong Baptist University, Hong Kong, China

    Ze-Guo Chen & Guancong Ma

  3. State Key Laboratory of Precision Measurement Technology and Instruments, Department of Precision Instrument, Tsinghua University, Beijing, China

    Hong-Bo Sun

Authors
  1. Xu-Lin Zhang
    View author publications

    Search author on:PubMed Google Scholar

  2. Feng Yu
    View author publications

    Search author on:PubMed Google Scholar

  3. Ze-Guo Chen
    View author publications

    Search author on:PubMed Google Scholar

  4. Zhen-Nan Tian
    View author publications

    Search author on:PubMed Google Scholar

  5. Qi-Dai Chen
    View author publications

    Search author on:PubMed Google Scholar

  6. Hong-Bo Sun
    View author publications

    Search author on:PubMed Google Scholar

  7. Guancong Ma
    View author publications

    Search author on:PubMed Google Scholar

Contributions

X.-L.Z. and G.M. conceived of the idea. X.-L.Z., Z.-G.C. and G.M. performed the theoretical analysis. X.-L.Z. performed numerical simulations and designed the experiment. F.Y. carried out the experimental measurements under the supervision of Z.-N.T. and Q.-D.C. The manuscript was written by X.-L.Z. and G.M. with inputs from all the authors. The project was supervised by G.M. and H.-B.S.

Corresponding authors

Correspondence to Xu-Lin Zhang, Zhen-Nan Tian, Hong-Bo Sun or Guancong Ma.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Notes 1–3, Figs. 1–12 and Table 1.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, XL., Yu, F., Chen, ZG. et al. Non-Abelian braiding on photonic chips. Nat. Photon. 16, 390–395 (2022). https://doi.org/10.1038/s41566-022-00976-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41566-022-00976-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing