1 Introduction

The Indian economy has developed at verifiably remarkable rates and is presently one of the fastest developing economies in the world. The country has progress appreciably to reform its economy, reduction hardship and fulfilling opportunities for everyday comfort for its widespread population. This continuous economic growth has also led to poverty reduction. Regardless of this noteworthy accomplishment, the income distribution in India remains intractably unequal. The movement of economy also directs the behavior of the labour market. The volatility in the economy, both in its inter and intra sectored linkages as well as in the context of economic integration with rest of the world, is reflected in the domestic labour market (MoSPI, 2020a). Global economic slowdown creates extreme volatility which can hugely influence the contemporary economic environment. Thus, it is immensely important to measure its short-term impact on labour market which requires the collection of labour force data at regular interval. In India, labour force participation in unorganized sector is much higher as compared to the organized sector. The frequent availability of labour force data was the need of the hour and that led to the launch of periodic labour force survey (PLFS) in 2017 by National Statistical Office (NSO), Ministry of Statistics and Program Implementation (MoSPI), Govt. of India. In India, NSO is the primary body to collect PLFS data for generating estimates at the state and the national level for both rural and urban areas. The PLFS data provides estimates for a range of employment and unemployment indicators such as unemployment rate, worker population ratio, labour force participation rate, earning of different working groups. Even though being extremely essential, the estimates of earning distribution are unachievable further down the state level in India e.g., district, block or further level of disaggregation.

Inequality creates barrier to growth and development when it denies people of opportunities which in turn, lead to the state of extreme poverty. There is a growing consensus that economic growth is not sufficient to reduce poverty if it is not inclusive and if it does not involve the three dimensions of sustainable development—economic, social and environmental, (UNDP, 2015). Goal 10 of sustainable development goal (SDG) aims that the income growth of the bottom 40% of country’s population is higher than the national average by the year 2030. The Gini coefficient of income inequality for India fell from 36.8% in 2010 to 33.6% in 2015. The Government of India prioritizes the policy of inclusion, financial empowerment and social security via major initiatives like Jan Dhan Yojona, Aadhaar etc. These comprehensive steps are in line with the SDG targets intended for achieving better equality and encouraging the socio-economic, and political inclusion of all by 2030. In the current situations, the growing interests of the policy makers, public agencies, scientists, government organization are focused in achieving the local (or micro) level estimates. The emphasis on disaggregate level SDG indicators by various national and international agencies has further lauded the inevitable need of such local level estimates. These local level areas or domains, better known as small areas or small domains are formed by cross-classification of several demographic and topographic variables that includes small topographic areas (e.g., districts) or small demographic groups (e.g., land category, social groups, religion, age-sex groups) or cross classifying both (Guha & Chandra, 2021a). Besides, in the existing PLFS data of NSO, the small areas or districts may have very small or even zero sample sizes which may lead to large sampling error in case of direct estimation. The SAE methodology provides a viable and cost-effective solution this problem of small sample sizes (Rao & Molina, 2015). The SAE techniques borrow strength from various external sources viz. time periods, areas etc. to obtain precise and reliable estimates.

The idea behind the SAE methodology is to link the variable under study with the auxiliary information through different statistical models which may leads to describe the model-based small area estimates corresponding to these small areas. Based on the availability of the auxiliary information, the unit level or the area level models are mostly used in SAE. The Fay–Herriot (FH) model (Fay & Herriot, 1979) is a widely accepted area level model in SAE when the model covariates are available only in aggregate form. The FH model assumes the availability of area specific survey estimates and these estimates follow an area level linear mixed model with area as random effects. Application of the FH model are readily available in literature in multiple dimensions. The uncertainty of the SAE estimates was deliberated by Prasad and Rao (1990), Datta et al. (2011). Fay (1987) and Datta et al. (1991) introduced the multivariate version of the FH model while Benavent and Morales (2016) extended it further. Often, there is a necessity of estimating correlated processes viz. poverty indicators, unemployment, etc. Multivariate models often allow for the correlation of several variables and usually suitable in these circumstances. Unlike the FH model, more than one variable of interest is modelled via multivariate Fay–Herriot model (MFH) by allowing for different covariance structure between the vector of the variable of interest and the random effects, see Guha and Chandra (2021b). A number of small area applications for estimating socio-economic indicators, poverty have been described in literature based on univariate FH model that ignores the correlation between the target variables, see for example, Chandra et al. (2011, 2020), and references therein. Furthermore, surveys are generally planned to collect information on more than a few variables. In SAE problem, when the target areas comprise insufficient sample size, taking into account of correlation between the target variables can provide an added advantage in obtaining precise and reliable small area estimates (Rao & Molina, 2015). Franco and Bell (2021) also pointed out that precision in bivariate area-level models is only improved if one of the outcomes has very low variance and the correlation between the two outcomes is very strong.

According to the quarterly report of MoSPI (2020b), the unemployment rate in the age group of 15 years and above has sharply increased from 9.1% in January–March 2020 to 20.8% in April–June 2020 with the working population ratio decreased from 43.7 to 36.4%. These figures indicate the severity of the job losses and sufferings faced by the majority of the working population in the country during the first phase of the COVID-19 pandemic. Given the severe economic hardships faced by a large section of the populations during this pandemic, having precise knowledge of district-level estimates of pre-pandemic earning distribution is critical for evaluating the true impact of the disaster. India reported the second highest number of COVID-19 cases for any country in the world (> 32 million) by mid-2021, with Uttar Pradesh contributing to almost 1.7 million cases (MoHFW, 2021). Uttar Pradesh, the most populous state in the country, accounts for about 17% of India’s population with an area of 241 thousand square km that equals to 8% of India’s total geographical area. About 29.43% population of the state lives below the poverty line which is higher than the national average of 21.92% (NITI Aayog, 2019). According to the Global Hunger Index 2020, out of 132 countries India stands on 94th position with an overall score of 27.2 (GHI, 2020). The state of Uttar Pradesh ranks 24th out of 28 states in “zero hunger” with a score of 41 which is much lower than the national average of 47 (NITI Aayog, 2019). In addition, 54.1% of the population is in the lowest two wealth quintiles in Uttar Pradesh and it ranks last out of 28 states in “reduced inequality” parameter with a score of 41 which is much lower than the national average of 67 (NITI Aayog, 2019). Therefore, it seems rational to consider Uttar Pradesh to generate the district level estimates of earning inequalities at rural and urban sectors using SAE techniques. To the best of our knowledge, no prior study has been done to estimate the disaggregate level earning inequalities in India.

The paper is organized as follows. Section 2 describes the data from the 2018–2019 Periodic labour force survey of the NSO of India and the 2011 Population Census of India that will be used to estimate the district level earning distribution in rural and urban sector of the Indian State of Uttar Pradesh. In Sect. 3, we set out the theoretical background of the area level MFH model, and then discuss the different variant of this model used in estimating small area means under this model. The results obtained from the application of district-level inequalities in earning distribution along with various diagnostic measures are reported in Sect. 4. We also provide spatial mapping of earning distribution in this section that serves to demonstrate the degree of district-level inequalities in the distribution of earning between rural and urban sector in Uttar Pradesh. Finally, Sect. 5 summarizes the paper and provides concluding remarks.

2 Data Description

In this segment, we introduce the major data sources utilized in multivariate SAE application. The 2018–2019 PLFS data of the NSO for rural and urban districts of Uttar Pradesh and the data from 2011 Population Census of India are used for estimating the district level inequality in the earning distribution between rural and urban sector of the state. The PLFS survey data is freely downloadable from the MoSPI, Government of India (http://mospi.nic.in/). Since 2017, NSO carries out the PLFS every year. In PLFS a rotational panel sampling design for first visit both in rural and urban areas and three periodic revisits in urban areas has been used while there was no revisit in rural areas. A stratified multistage survey design was adopted, with the ultimate units being households. The 2018–2019 PLFS of NSO is intended to produce precise and reliable estimates at the state and the national level for both rural and urban areas in the country. However, at district level, this PLFS data cannot directly be used to generate precise and reliable estimates, since sample size within each district is not adequate to offer district-level estimates with acceptable reliability and precision. Although, district is always being a very crucial part of the planning process in the country, there are no surveys conducted to produce district level estimates in India and this leads to limit the policy interventions at the district or even further lower level (Guha & Chandra, 2021b).

The 2018–2019 PLFS data of the NSO comprised 28,132 persons in 5822 households from the rural and urban areas in 71 districts of Uttar Pradesh. For all the districts, the sample size ranges from 18 to 199 with an average of 85 for rural areas while for urban areas, it is 6–321 with an average of 57. This survey provides information on earning estimate of every person separately for rural and urban areas in Uttar Pradesh. Districts included moderately small sample sizes with an average sampling fraction of 0.000054 for rural and 0.00011 for urban areas. “On account of the constraint of small sample size, it is not possible to produce precise and reliable direct estimates at district level and subsequently leads to producing large standard errors from this survey” (Chandra et al., 2011; Rao & Molina, 2015). In this paper, we made an effort to address the problem of small sample size in achieving district-level estimates from the 2018–2019 PLFS data. The multivariate small area method has been applied to tackle this problem by including related covariates from the Population Census 2011 of India.

We have considered the following information on earning from employment from PLFS 2018–2019 viz. (a) self-employed persons, (b) salaried employees and regular wage earner, and (c) person working as casual labour. For salaried employees and regular wage earner in current weekly status (CWS), information on earnings in the previous calendar month was collected. For self-employed persons in CWS, information on earnings in the last 30 days from the self-employment was collected. It is important to note that average gross earnings from the self-employment activity have been calculated by excluding those self-employed persons who had reported earning as zero or not reported. For the person working as casual labour (except public works), information on earnings was collected for the casual labour work in which the person was engaged for each and every day of the reference week i.e., last 7 days prior to the date of the survey. For the sake of the analysis, we have transformed the daily data into monthly data for the casual labour work. The estimates in this section are derived using the data collected in the first visit schedules in the rural areas (since there was no revisit in rural areas) and for the urban areas using the data collected in the schedules of first visit and the corresponding revisits conducted during the four quarters of the survey period, viz., during July–September followed by October–December in 2018 and January–March followed by April–June in 2019. For more detailed information on the method of the data collection, readers may refer to the annual report of the PLFS 2018–2019 (MoSPI, 2020a). The target variables in the 2018–2019 PLFS data are Y1: average monthly Earning (in Rs.) of a person from employment in rural areas (hereafter denoted by Rural), Y2: average monthly Earning (in Rs.) of a person from employment in urban areas (hereafter denoted by Urban). This paper targets to estimate the inequality in average monthly earning of a person in rural and urban districts in Uttar Pradesh at small area level through joint modelling of the target variables i.e., Rural and Urban.

3 Multivariate Small Area Modelling

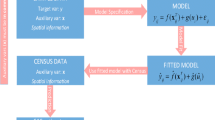
In what follows, we briefly describe multivariate SAE methodology applied in the estimation of district level inequality in distribution of average monthly earning. Let us assume that the population consists M small areas or areas (districts in this analysis) and let there are R number of target variables in this study. All the way through, a subscript \(m(m = 1, \ldots ,M)\) is used to denote the quantities possess by small area m and a subscript \(r(r = 1, \ldots ,R)\) is used to index the variable r under study. Assume a finite population \(\Omega\) of size N comprises M non-overlapping domains \(\Omega_{m} \,;m = 1, \ldots ,M\) and a sample s of size n is drawn from \(\Omega\) by any probability sampling design. We also assume that the domain size \(N_{m}\) is known for each domain and \(n_{m}\) units are selected in the sample from \(N_{m}\) units of mth domain (hereafter denoted by small area). The population total is given by \(N = \sum\nolimits_{m = 1}^{M} {N_{m} }\) and the corresponding sample size is \(n = \sum\nolimits_{m = 1}^{M} {n_{m} }\). Let \(y_{mrj}\) be the value corresponding to jth unit of the rth target variable in mth area, \(r = 1, \ldots ,R\), \(j = 1, \ldots ,N_{m}\) and \(m = 1, \ldots ,M\). The aim is to estimate small area mean \(\overline{Y}_{mr} = N_{m}^{ - 1} \sum\nolimits_{{j \in \,\Omega_{m} }} {y_{mrj} }\), \(r = 1, \ldots ,R\) and \(m = 1, \ldots ,M\). The traditional direct survey estimator (hereafter denoted by Direct) for \(\overline{Y}_{mr}\) is given by \(\overline{y}_{mr} = \sum\nolimits_{j = 1}^{{n_{m} }} {\tilde{w}_{mrj} y_{mrj} }\) with \(\tilde{w}_{mrj} = {{w_{mrj} } \mathord{\left/ {\vphantom {{w_{mrj} } {\sum\nolimits_{j = 1}^{{n_{m} }} {w_{mrj} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{j = 1}^{{n_{m} }} {w_{mrj} } }}\) where \(\tilde{w}_{mrj}\) is the normalized survey weight for jth unit of the rth variable in mth area. In addition, \(\tilde{w}_{mrj}\) satisfies \(\sum\nolimits_{j = 1}^{{n_{m} }} {\tilde{w}_{mrj} } = 1\) with \(w_{mrj}\) being the survey weight for jth unit of the rth variable in mth area. Following Särndal et al. (1992), the estimated variance of Direct estimator is approximated by \(v\left( {\overline{y}_{mr} } \right) = \sum\nolimits_{j = 1}^{{n_{m} }} {\tilde{w}_{mrj} \left( {\tilde{w}_{mrj} - 1} \right)\left( {y_{mrj} - \overline{y}_{mr} } \right)}^{2}\). Under simple random sampling without replacement (SRSWOR), \(w_{mrj} = {1 \mathord{\left/ {\vphantom {1 {\pi_{mrj} }}} \right. \kern-\nulldelimiterspace} {\pi_{mrj} }}\) where \(\pi_{mrj} = {{n_{m} } \mathord{\left/ {\vphantom {{n_{m} } {N_{m} }}} \right. \kern-\nulldelimiterspace} {N_{m} }}\) is the inclusion probability for jth unit of the rth variable in the mth area.

Let us further assume that \(y_{mr} (r = 1, \ldots ,R)\) be an unbiased direct survey estimator of an unknown population parameter (e.g., the population mean) \(Y_{mr}\) of the target variable r for small area m. Let \({\mathbf{x}}_{mr}\) be a \(p_{r}\)-vector of available auxiliary variables corresponding to area m that are associated to the population mean \(Y_{mr}\) for the variable r under study. Usually, area-specific auxiliary informations are acquired from some available secondary sources, for example, administrative registers, the population census, etc. We denote \({\mathbf{y}}_{m} = \left( {y_{1r} ,...,y_{mr} } \right)^{T}\), a vector of direct survey estimators of \({\varvec{Y}}_{m}\) where \({\varvec{Y}}_{m}\) is the m-vector population mean of target variables. In line with Benavent and Morales (2016), an area-level FH model (Fay & Herriot, 1979) used for more than one target variables is given by

$$ {\mathbf{y}}_{m} = {\varvec{Y}}_{m} + {{\varvec{\upvarepsilon}}}_{m} \quad {\text{and}}\quad {\varvec{Y}}_{m} = {\mathbf{X}}_{m} {{\varvec{\upbeta}}} + {\mathbf{u}}_{m} $$
(1)

In literature, the model in (1) is time and again referred to the multivariate form of the FH model. The MFH model in (1) consists of two stage, the first one takes care of the sampling variability of the direct survey estimates \({\mathbf{y}}_{m}\) of true area means of the target variable \({\varvec{Y}}_{m}\) while the second stage accounts for linking of the true area means of the target variable \({\varvec{Y}}_{m}\) to \({\mathbf{X}}_{m} = diag\left( {{\mathbf{x}}_{m1} , \ldots ,{\mathbf{x}}_{mR} } \right)_{R \times p}\), a matrix of available auxiliary variables where \(p = \sum\nolimits_{r = 1}^{R} {p_{r} }\). This model in (1) can be denoted as an area level random effect model as

$$ {\mathbf{y}}_{m} = {\mathbf{X}}_{m} {{\varvec{\upbeta}}} + {\mathbf{u}}_{m} + {{\varvec{\upvarepsilon}}}_{m} ,\;m = 1, \ldots ,M $$
(2)

here \({{\varvec{\upbeta}}} = \left( {{\mathbf{\beta^{\prime}}}_{1} , \ldots ,{\mathbf{\beta^{\prime}}}_{r} } \right)^{\prime }_{p \times 1}\) and \({{\varvec{\upbeta}}}_{r}\) is a \(p_{r}\)- vector of unknown fixed effect parameters. The vector of random area effects \({\mathbf{u}}_{m}\) are independent and identically distributed with \({\mathbf{u}}_{m} \mathop \sim \limits^{ind} N\left( {0\,,\,\,{\mathbf{V}}_{{u_{m} }} } \right)\) while vectors of sampling errors \({{\varvec{\upvarepsilon}}}_{m}\) are independent and normally distributed with \({{\varvec{\upvarepsilon}}}_{m} \sim N\left( {0\,,\,\,{\mathbf{V}}_{{\varepsilon_{m} }} } \right)\). Moreover, these two vector of errors \({\mathbf{u}}_{m}\) and \({{\varvec{\upvarepsilon}}}_{m}\) are independent of each other within and between areas with \({\mathbf{V}}_{{\varepsilon_{m} }}\), the covariance matrices of \({{\varvec{\upvarepsilon}}}_{m}\) are known while the covariance matrices of \({\mathbf{u}}_{m}\) denoted by \({\mathbf{V}}_{{u_{m} }}\) depend on unobservable parameters \({{\varvec{\uptheta}}} = \left( {\theta_{1} , \ldots ,\theta_{R} } \right)\). Combining M-area-level models, the model in (2) can be denoted in matrix form as

$$ {\mathbf{y}} = {\mathbf{X\beta }} + {\mathbf{Zu}} + {{\varvec{\upvarepsilon}}}, $$
(3)

where \({\mathbf{y}} = {\text{col}}\left( {{\mathbf{y}}_{m} ;1 \le m \le M} \right)\) is the vector of direct estimates of order \(MR \times 1\), \({\mathbf{X}} = {\text{col}}\left( {{\mathbf{X}}_{m} \,;\,1 \le m \le M} \right)\) is the matrix of known covariates of dimension \(MR \times p\), \({\mathbf{Z}} = {\text{col}}^{{\prime }} \left( {{\mathbf{Z}}_{m} ;1 \le m \le M} \right)\) is the \(MR \times MR\) matrix of known covariates illustrating differences between the small areas, \({\mathbf{u}} = {\text{col}}\left( {{\mathbf{u}}_{m} \,;\,1 \le m \le M} \right)\) is the vector of random area effects of dimension \(MR \times 1\) and \({{\varvec{\upvarepsilon}}} = {\text{col}}\left( {{{\varvec{\upvarepsilon}}}_{m} \,;\,1 \le m \le M} \right)\) is the vector of sampling errors of dimension \(MR \times 1\) with \({\mathbf{u}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{u} } \right)\) and \({{\varvec{\upvarepsilon}}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{\varepsilon } } \right)\). At large, \({\mathbf{Z}}\) is denoted a matrix whose mth column \({\mathbf{Z}}_{m}\), \(m = 1, \ldots ,M\), is an indicator variable which takes the value 1 if a unit belongs to an area m and zero otherwise. Especially, in model (3) \({\mathbf{Z}}\) is a \(MR \times MR\) diagonal matrix. Furthermore, it is supposed that the random area effects \({\mathbf{u}}\) are independently distributed of the sampling errors \({{\varvec{\upvarepsilon}}}\) where \({\mathbf{u}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{u} } \right)\) and \({{\varvec{\upvarepsilon}}} \sim N\left( {0\,,\,\,{\mathbf{V}}_{\varepsilon } } \right)\). The random effects covariance matrix is denoted by \({\mathbf{V}}_{u} = {\text{diag}}\left( {{\mathbf{V}}_{um} \,;\,1 \le m \le M} \right)\) and \({\mathbf{V}}_{\varepsilon } = {\text{diag}}\left( {{\mathbf{V}}_{\varepsilon m} \,;\,1 \le m \le M} \right)\) is the matrix of design variances.

Next we consider three types of the model (3) to obtain model-based small area estimates. First, we take \({\mathbf{V}}_{{u_{m} }} = {\text{diag}}\left( {\sigma_{ur}^{2} \,;\,1 \le r \le R} \right)\), \({\mathbf{V}}_{{\varepsilon_{m} }} = {\text{diag}}\left( {\sigma_{\varepsilon mr}^{2} \,;\,1 \le r \le R} \right)\), \(m = 1, \ldots ,M\) and \(\sigma_{\varepsilon mr}^{2}\)’s are known for the estimator based on univariate FH model (UFH). Second estimator, denoted by MFH-1, is based on MFH model with \({\mathbf{V}}_{{u_{m} }} = {\text{diag(}}\sigma_{ur}^{2} ;1 \le r \le R)\), \(m = 1, \ldots ,M\), and a known but not necessarily diagonal matrix \({\mathbf{V}}_{\varepsilon }\). The third estimator, denoted by MFH-2, is also based on MFH model where the random effects \({\mathbf{u}}_{m} = \left( {{\mathbf{u}}_{m1} ,\,.\,.\,.,\,{\mathbf{u}}_{mR} } \right)^{\prime }\) is generated via a first order heteroscedastic autoregressive HAR(1) process \({\mathbf{u}}_{mr} = \rho {\mathbf{u}}_{mr - 1} + {{\varvec{\uptau}}}_{mr}\) with \({\mathbf{u}}_{m0} \sim N\left( {0\,,\,\,\sigma_{0}^{2} } \right)\), \({{\varvec{\uptau}}}_{mr} \sim N\left( {0\,,\,\,\sigma_{r}^{2} } \right)\), \(r = 1, \ldots ,R\) and \(\sigma_{0}^{2}\), \({\mathbf{u}}_{m0}\), \({{\varvec{\uptau}}}_{mr}\) are independent. The components of \({\mathbf{V}}_{{u_{m} }}\) are given by \(\sigma_{umii} = \sum\nolimits_{k = 0}^{i} {\rho^{2k} \sigma_{i - k}^{2} }\) and \(\sigma_{umij} = \sum\nolimits_{k = 0}^{{\left| {j - i} \right|}} {\rho^{{2k + \left| {j - i} \right|}} \sigma_{{\left| {j - i} \right| - k}}^{2} } ,\,\,\,i \ne j\) and it is assumed that sampling errors are not independent with each other i.e., \({\mathbf{V}}_{\varepsilon }\) is known but not essentially a diagonal matrix. For UFH and MFH-1 estimators, the number of unknown variance component parameters to be estimated is equal to \(R\) with \(\theta_{r} = \sigma_{ur}^{2} ,\,\,r = 1, \ldots ,R\) and for MFH-2, it is \(R + 1\) with \(\theta_{r} = \sigma_{ur}^{2} ,\)\(r = 1, \ldots ,R\) and \(\theta_{R + 1} = \rho\). Under the model (3), \(E\left( {\mathbf{y}} \right) = {\mathbf{X\beta }}\) and \(Var\left( {\mathbf{y}} \right) = {\mathbf{V}}_{y} = {\mathbf{V}}_{u} + {\mathbf{V}}_{\varepsilon } = diag\left( {{\mathbf{V}}_{ym} \,;\,1 \le m \le M} \right)\), with \({\mathbf{V}}_{u} = {\mathbf{Z^{\prime}}}\,{\mathbf{V}}_{u} {\mathbf{Z}}\) and \({\mathbf{V}}_{ym} = {\mathbf{V}}_{um} + {\mathbf{V}}_{\varepsilon m} \,,\,\,m = 1, \ldots ,M\). Here, the covariance matrix \({\mathbf{V}}_{y}\) depends on \(R\) and \(R + 1\) unknown variance component parameters given by \({{\varvec{\uptheta}}} = \left( {\theta_{1} ,\,\,.\,\,.\,\,.,\,\,\theta_{R} } \right)\) for UFH and MFH-1 and \({{\varvec{\uptheta}}} = \left( {\theta_{1} , \ldots ,\theta_{R + 1} } \right)\) for MFH-2 model respectively. The restricted maximum likelihood (REML) method is applied to estimate \({{\varvec{\uptheta}}}\). Replacing the estimated values \({\hat{\mathbf{\theta }}}\) of parameters \({{\varvec{\uptheta}}}\) in \({\mathbf{V}}_{u}\) to obtain \({\hat{\mathbf{V}}}_{u} = {\mathbf{V}}_{u} ({\hat{\mathbf{\theta }}})\) and \({\hat{\mathbf{V}}}_{y} = {\hat{\mathbf{V}}}_{u} + {\mathbf{V}}_{\varepsilon }\), the multivariate version of empirical best linear unbiased predictors (EBLUP) of \({\varvec{Y}}\) is defined as

$$ \hat{\user2{Y}}_{{{\text{MFH}}}} = {\mathbf{X}}{\hat{\mathbf{\beta }}} + {\mathbf{Z}}{\hat{\mathbf{u}}}{\mathbf{.}} $$
(4)

Here, the empirical best linear unbiased estimator (BLUE) of \({{\varvec{\upbeta}}}\) and the EBLUP of \({\mathbf{u}}\) are obtained as \({\hat{\mathbf{\beta }}} = \left( {{\mathbf{X^{\prime}}}\,{\hat{\mathbf{V}}}_{y}^{ - 1} {\mathbf{X}}} \right)^{ - 1} {\mathbf{X^{\prime}}}\,{\hat{\mathbf{V}}}_{y}^{ - 1} {\mathbf{y}}\) and \({\hat{\mathbf{u}}} = {\hat{\mathbf{V}}}_{u} {\mathbf{Z^{\prime}}}\,{\hat{\mathbf{V}}}_{y}^{ - 1} \left( {{\mathbf{y}} - {\mathbf{X\hat{\beta }}}} \right)\) respectively. In small area applications, the mean squared error (MSE) estimates are desirable to measure the precision of estimates and also to construct the confidence interval for the estimates (Guha & Chandra, 2021b). The analytical MSE estimate of EBLUP of MFH in (4) is obtained following Benavent and Morales (2016).

4 Results and Discussions

4.1 Variable Selection and Model Fitting

We used Population Census, 2011 data of India for selection of suitable covariates for small area modelling. As these covariates are available as counts at district level, area-level multivariate small area models were used in this analysis to obtain the small area estimates. There are almost 30 auxiliary variables are accessible from the census data and we did some exploratory analysis prior to selection of appropriate covariates for multivariate small area model fitting. A stepwise regression is performed for choosing significant auxiliary variables based on Akaike information criterion (AIC) value. Initially, the direct estimates of two target variables i.e., Rural and Urban are plotted to get an impression about the correlation between them. From Fig. 1, it seems that these two target variables Rural and Urban are loosely correlated. Note that, for the target variable Urban, there was 05 non-sample districts for which no information is available related to earning. Consequently, we fit a FH model with the sample areas and then a synthetic estimation (see Chandra et al., 2011) is carried out to estimate the non-sample areas in urban districts. MSE of the synthetic estimates are obtained following Chandra et al., (2011).

Fig. 1
figure 1

Scatter plots of the direct estimates of Rural and Urban

Full size image

Next, we proceed with the MFH-2 model described in the previous section using direct estimates of Rural and a combination of the direct estimates and the synthetic estimates of Urban corresponding to the sample and the non-sample areas as the input of the two target variables and some selected covariates from the census data as suitable auxiliary variables. Finally, three significant covariates viz. main worker population (MWP), Cultivator population (CP) and marginal casual labour population (MCP) corresponding to the target variable Rural and for Urban, three significant covariates viz. literacy rate (LR), main worker population (MWP) and marginal casual labour population (MCP) are included in the model based on the AIC value. The regression parameter estimates are reported in Table 1 for the two dependent variable Rural and Urban. Observing the signs of the regression parameters estimates, it can be concluded that rural districts having lesser proportion in the covariate CP and greater proportion in MWP and MCP covariates have more earning while urban districts having greater proportion in all the three significant covariates have more earning.

Table 1 Regression parameters, Standard error and p-values for the target variables Rural and Urban
Full size table

The values of estimates from fitting the multivariate small area model in 2018–2019 PLFS data are described as follows. The estimate of variance component parameters for the MFH-2 model are \(\hat{\sigma }_{u1}^{2} = 1247400\), \(\hat{\sigma }_{u2}^{2} = 11161000\) and \(\hat{\rho } = - 0.3271\). We also test the null hypothesis \(H_{0} :\sigma_{ui}^{2} = \sigma_{uj}^{2}\), \(i,\,j\, = 1,\,\,2,\,\,i \ne j\) against the alternative hypothesis \(H_{1} :\sigma_{ui}^{2} \ne \sigma_{uj}^{2}\). The test statistic is given by \(t_{ij} = {{\hat{\sigma }_{ui}^{2} - \hat{\sigma }_{uj}^{2} } \mathord{\left/ {\vphantom {{\hat{\sigma }_{ui}^{2} - \hat{\sigma }_{uj}^{2} } {\sqrt {\upsilon_{11} + \upsilon_{22} - 2\upsilon_{12} \,} }}} \right. \kern-\nulldelimiterspace} {\sqrt {\upsilon_{11} + \upsilon_{22} - 2\upsilon_{12} \,} }}\,\,\,;\,\,\,i,\,j\, = 1,\,\,2,\,\,i \ne j\), where \(\upsilon_{rs} \,,\,\,r,\,s\, = 1,\,\,2\) are the elements of the inverse of the matrix of Fisher information corresponding to the MFH-2 model calculated at \({\hat{\mathbf{\theta }}} = \left( {\hat{\sigma }_{u1}^{2} ,\,\,\hat{\sigma }_{u2}^{2} ,\,\,\hat{\rho }} \right)\). The value of test statistic is given by \(t_{12} = - 3.8803\,\left( { < 0.001} \right)\) with p-value given in parenthesis. As the value of the test statistic is significant at 5% level, this leads to the conclusion that variance of random area effects for Rural and Urban are significantly different. This followed by testing \(H_{0} :\rho = 0\) with the test statistic \(t_{\rho } = {{\hat{\rho }} \mathord{\left/ {\vphantom {{\hat{\rho }} {\sqrt {\upsilon_{33} \,} }}} \right. \kern-\nulldelimiterspace} {\sqrt {\upsilon_{33} \,} }}\) and the value of \(t_{\rho } = - 0.6208\left( {0.2673} \right)\), p-value is in parenthesis. This reveals that the correlation between the two target variables is not significantly different from zero and we go with MFH-1 model with diagonal covariance matrix instead of MFH-2 model. It is important to note that, although the variance of random area effects for Rural and Urban are significant at 1% level, the correlation between the two target variables is not significantly different from zero. This leads to the almost identical results in univariate and multivariate estimates which established the idea reported in Franco and Bell (2021) that that precision in multivariate area-level models is only improved if one of the outcomes has very low variance and the correlation between the two outcomes is very strong. Finally, the MFH-1 model is applied with all the significant auxiliary variables to obtain the earnings estimates i.e., Rural and Urban for all the districts in Uttar Pradesh.

4.2 Diagnostic Measures

In what follows, we described some standard diagnostic measures to examine the model assumptions and inspect the reliability and validity of the generated estimates through MFH method. In line with, Brown et al. (2001), two forms of diagnostics viz. (a) the model diagnostics, and (b) the multivariate SAE diagnostics are employed to endorse the model assumptions. The reliability of the model-based estimates of Rural and Urban attained by SAE method under MFH-1 model is validated by some additional diagnostics. Corresponding to the target variable Rural and Urban, the random effects in MFH-1 model are supposed to follow a normal distribution with 0 mean and constant variance \(\sigma_{ur}^{2}\), \(r = 1,\,2\). If the underlying model assumptions hold, the residuals are supposed to be distributed randomly around zero. We used the normal probability (Q-Q) plots to examine the normality assumption. Q-Q plots of district level residuals corresponding to the two target variables Rural and Urban are given in Fig. 2. In addition, we also examined the normality assumption of the random area effects via Shapiro–Wilk test and the p-values of the test are 0.138 and 0.445 for Rural and Urban respectively. Furthermore, it is evident from the Q-Q plot in Fig. 2 that the normality assumption holds while p-values of the test are greater than 0.05 and both of these evidences taken together indicate that the district wise random area effects are likely to be distributed normally. Next, we evaluated the validity and the reliability of the small area estimates by some frequently used diagnostics. In line with Brown et al. (2001) and Chandra et al. (2011), model-based small area estimates should be (1) consistent with unbiased direct survey estimates and (2) more efficient than direct estimates in terms of MSE. The subsequent measures e.g., the bias diagnostic, the percentage coefficient of variation (CV) and the 95% confidence interval (CI) are selected. Later, we classified the measurements of CV and CI as internal diagnostic measures as these indicate the efficiency of the small area estimates. Moreover, a calibration diagnostic is also applied in which the model-based small area estimates are combined to an upper level so that these estimates can be compared with direct estimates at that higher level and we classified this as an external diagnostic measure. It is important to note that in this case, the direct estimates are in survey weighted form.

Fig. 2
figure 2

Normal Q-Q plot of district-level residuals for Rural (on the left) and Urban (on the right)

Full size image

4.2.1 Bias Diagnostic

The bias diagnostic measure test the validity while the precision of the model-based estimates are examined by the CI and CV. Following Chandra et al. (2011), the bias diagnostic is performed. Being unbiased of the population values, the regression of the direct estimates on the true population values likely to be linear with the identity line. If the model-based estimates are close to these true values of the population, the regression of direct estimates on model-based small area estimates expected to be similar. Consequently, we plotted the direct estimates and model-based estimates in the y and x-axis respectively and examined the departure of the small area estimates from the regression line fitted values. The plot given in Fig. 3 demonstrates that small area estimates are not as extreme as the direct estimates signifying the usual SAE result of diminishing greater extreme values to the average values and the value of R2 were 0.91 and 0.94 for Rural and Urban respectively. Largely, this diagnostic specify that the small area estimates are expected to be consistent when compared with direct estimates. This is expected as the MFH estimates are realization of random variables and so the regression of the direct estimates on the MFH estimates is unbiased for a test of common expected values.

Fig. 3
figure 3

Bias diagnostic plot with y = x line (thin line) and regression line (solid black line) for Rural (on the left) and Urban (on the right)

Full size image

4.2.2 Internal Diagnostic

Afterward, the degree of improvement in precision of model-based small area (i.e., district level) estimates of Rural and Urban are examined against the FH and direct survey estimates. Typically, small area estimates having smaller CVs are likely to be reliable. The summary of %CVs of the Direct, FH and MFH estimates of Rural and Urban are given in Table 2 and the corresponding CV ratio is given in Fig. 4. District specific %CV is demonstrated in Fig. 5. The direct survey estimates possess greater CV compared to the FH and MFH estimates of Rural and Urban. It is obvious from Table 2 and Fig. 5 that direct survey estimates of Rural and Urban seem to be highly unstable. It is important to note that, for the target variable Urban, there was 05 non-sample districts. So, for Urban we first compare the performance with the sampled districts and comparison of non-sample districts are given separately. For Rural, the CV of Direct distributed from 3.98 to 28.61% with a median value of 9.58% whereas it is 3.83–14.96% with a median value of 8.34% for MFH which indicate that the MFH estimates are more strongly distributed compared to the direct estimates. Similarly for Urban, when we compare the Direct with MFH for the 66 sampled districts, the CV of Direct is distributed from 1.69 to 31.25% with a median value of 13.45% whereas it is 1.68–21.85% with a median value of 12.48% for MFH. Furthermore, when FH and MFH estimates are compared, the performance seems to be similar in case of Rural where there was no non-sampled district. However, in case of Urban with 05 non-sampled district, the CV of FH is distributed from 26.18 to 55.99% with a median value of 37.65% for the non-sampled districts while it is 18.61–41.29% with a median value of 26.93% for MFH estimates. It seems clear From Fig. 5, with decreasing sample sizes of the districts the relative performance of the MFH estimates for Rural and Urban has improved. Accordingly, these precise and reliable MFH estimates generate the district level earning estimate much better than direct and FH estimates. The 95% confidence intervals (CIs) are given in Fig. 6. The Fig. 6 indicate that the CI of MFH estimate is much tighter than the direct survey estimates.

Table 2 Distribution of % CV for the direct and model-based small area estimates of Rural and Urban
Full size table
Fig. 4
figure 4

CV ratio of Direct to FH (Red) and Direct to MFH (Blue) estimates for Rural (at the top) and urban (at the bottom). (Color figure online)

Full size image
Fig. 5
figure 5

District specific percentage coefficient of variation (CV) of Direct (Black, °) and MFH (Red, □) estimate for Rural (in left) and Urban (in right). Districts are arranged in increasing order of sample size. (Color figure online)

Full size image
Fig. 6
figure 6

District-wise 95% nominal confidence interval for the Direct (Black) and MFH (Red) estimates for Rural (on the left) and urban (on the right). Districts are arranged in increasing order of direct estimates. (Color figure online)

Full size image

4.2.3 External Diagnostic

The aggregation property of the MFH based district-level SAE estimates at higher aggregation level viz. state and regional level) are examined. The regional and state-level estimates of Rural and Urban is obtained by.

\(\hat{Y}_{i} = {{\sum\nolimits_{j = 1}^{M} {N_{j} \hat{Y}_{ij} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{j = 1}^{M} {N_{j} \hat{Y}_{ij} } } {\sum\nolimits_{j = 1}^{M} {N_{j} } }}} \right. \kern-\nulldelimiterspace} {\sum\nolimits_{j = 1}^{M} {N_{j} } }}\), \(i = 1,\,\,2\) and \(j = 1, \ldots ,M\),where \(\hat{Y}_{ij}\) denote the MFH estimate of Rural and Urban for \(i = 1,\,\,2\) and district j and the population size is \(N_{j}\) corresponding to the jth district. The districts are classified in four regions i.e. Central, Southern, Eastern and Western regions and we studied the aggregation property. The state and the regional-level estimates of Rural and Urban are reported in Table 3. While comparing the small area estimates against the direct estimates, it seems that in both the state and the regional level these small area estimates are close enough to the direct estimates.

Table 3 Aggregated estimates of Rural and Urban obtained from Direct and MFH. Estimates are aggregated over 71 districts for rural areas and 66 districts for urban areas at the state and regional levels
Full size table

4.3 Spatial Distribution of Earning Inequality

Tables 4 and 5 report the distribution of CV and earning range across all the districts respectively. The district specific direct survey estimates and MFH estimates together with the 95% CI and CV for Rural and Urban are given in Tables 6 and 7. The spatial maps of earning (in Rs) by districts for both rural and urban areas are produced for the district level estimates generated by MFH method. Figure 7 displays spatial maps of the MFH estimates of earning for Rural and Urban areas of Uttar Pradesh. These spatial mapping assist in describing the magnitude of inequality in earning distribution between the district of rural and urban areas of the state. In case of rural areas, western region in Uttar Pradesh has lower earning followed by the central and eastern region. For urban areas, the lower earning level exist in central region followed by the eastern and western region. The average monthly earning is ranging from Rs. 4518 to 11,827 in rural areas whereas it is Rs. 3424 to Rs. 19,809 in urban areas. This clearly indicate that there is a huge difference in average monthly earning between rural and urban areas in Uttar Pradesh. Moreover, from Table 4 and Fig. 7, MFH estimates also reveal that number of districts having average monthly earning of Rs. 10,000 or more is only 02 in rural areas while it is 46 for urban areas. In case of lower earning level, 38 districts in rural areas showing average monthly earning of Rs. 7500 or less whereas it is only 07 districts for urban areas. Table 4 further described that almost 97% of rural areas possess an average monthly earning of Rs. 7500 or less however nearly 89% of urban areas hold an an average monthly earning of more than Rs. 7500. Taken together, it is evident from these results that the degree of earning inequality between rural and urban districts is extremely severe and clearly visible. The difference in earning in rural and urban areas of Uttar Pradesh can be obtained from Tables 6 and 7 and we may conclude that out of 71 districts in Uttar Pradesh, 06 districts in rural areas are having earning higher than urban areas. But this seems not be the case as the direct estimates for urban areas in these 06 districts are truly unstable with higher CV percentage. Districts viz. Jyotiba Phule Nagar, Kannauj, Etawah, Chitrakoot, Fatehpur and Faizabad indicate higher level of earning in rural areas compared to urban. Sample sizes for rural areas in these districts also indicate that these particular districts covered more rural parts than the urban areas for which sample sizes are nearly tends to zero. These spatial maps and results provide useful information to policymakers in effective policy formulation and financial planning.

Table 4 Distribution of CV of 71 districts in rural areas and 66 districts in urban areas
Full size table
Table 5 Distribution of earning range of 71 districts in rural and urban areas based on MFH estimates
Full size table
Table 6 Direct and MFH estimates along with 95% confidence interval (95% CI) and percentage coefficient of variation (CV) of the target variable Rural by District in Uttar Pradesh
Full size table
Table 7 Direct and MFH estimates along with 95% confidence interval (95% CI) and percentage coefficient of variation (CV) of the target variable Urban by District in Uttar Pradesh
Full size table
Fig. 7
figure 7

Model-based MFH estimates displaying the spatial distribution of earning inequality by District between rural (on the left) and urban (on the right) areas in Uttar Pradesh

Full size image

5 Conclusion

According to UNDP (2015), earning inequality has increased by 11% in developing countries during 1990–2010 and 27.5% of the population in India are multidimensionally poor. World Bank (2020) reported that almost 21% of the India’s population living in extreme poverty in 2017 while India accounts for 17.8% of the world population (World Bank, 2019) which reveals that India’s share of the world’s extreme poor population is greater than its share of the world population. Like all the major developed countries around the world, the COVID-19 pandemic has also hit the India’s economy very hard with the loss of millions of jobs, causing in considerably reduced household incomes and extreme poverty. Due to the socioeconomic and health crisis in this pandemic, India’s economy has experienced the biggest annual contraction of 7.3% in its gross domestic product (MoSPI, 2021) since independence. As part of the 2030 Agenda for sustainable development, the first target of the 10th goal is “By 2030, progressively achieve and sustain income growth of the bottom 40% of the population at a rate higher than the national average”. After the major economic reforms in India during 1990s, the share in total earning of the top 1% is continuously increasing while the share in total earning of the bottom 50% started declining. To implement the agenda of sustainable development, India currently lacks the critically essential disaggregate level measures and maps of localized earning inequality.

At the outset of this paper, the multivariate Fay–sHarriot model (MFH) and its corresponding empirical best linear unbiased predictor are summarized. Then we applied this method in the 2018–2019 PLFS data of NSO, Govt. of India to produce the model-based estimate and spatial mapping of earning inequalities in rural and urban areas of Uttar Pradesh. For selection of suitable covariates, data from 2011 Population Census of India are used and we applied stepwise regression technique for choosing significant covariates. “Efficient estimation of correlated measures like food insecurity, nutritional consumption disparities are often required multivariate modelling approach which takes into account for the correlation between the target variables” (Guha & Chandra, 2021b). In this analysis, both the target variables viz. Rural and Urban are jointly modelled via MFH model and the gain is achieved in terms of MSE and CV for the target variables Rural and Urban. These estimates related to earning inequalities across the state of Uttar Pradesh can assist in motivating the dialogue about the drivers of earning inequalities in this state. Various diagnostic methods were used to assess the model-based MFH estimates and it also reveals significant gains in efficiency in producing district level estimates of earning which consequently measures the distribution of inequality persist between rural and urban areas in the state. Moreover, the spatial maps so obtained show the evidence of unequal earning distribution across the districts of rural and urban areas in Uttar Pradesh. Districts such as Shajahanpur, Faizabad, Sonbhadra exhibit lower level of earning to a great extent and demonstrate very high-level inequality whereas districts like Gonda, Ghaziabad, Etawah revealed high level of earning in the state.

This study indisputably recognized the benefits of SAE technique to tackle the small sample size problem when we want to obtain cost effective and precise disaggregate level estimates together with the confidence intervals from the existing PLFS data. In addition, this study also reveals the advantages of MFH over FH model in case of non-sample districts. This analysis also established the fact that many areas in rural sector of Uttar Pradesh possess very low level of earning compared to the urban sector and the earning gap is clearly visible from this study. The NSO surveys of Government of India are intended for obtaining state and national level estimates and these surveys do not reveal the real situation at the micro level (for example block or district level). Substantial importance is given on micro level planning by the Government of India for realizing a stable economic development together with earning generation. For definite planning and development in a country, district is always an important purview and thus availability of district-level data and statistics are very much vital for planning and monitoring of policy action plans. These cost effective and precise model-based estimates together with spatial maps may be useful for various and Ministries and Departments in Government of India along with international organizations for effective policy planning and monitoring related to sustainable development goal 10—reduced inequalities. This study can assist in obtaining the district level estimates and examine the inequality in earning distribution in the remaining parts of the country. Moreover, as earning data are generally skewed in nature, authors are working to handle this problem in multivariate SAE framework.