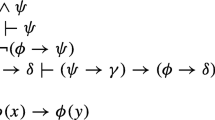Why classical logic is privileged: justification of logics based on translatability

Abstract

In Sect. 1 it is argued that systems of logic are exceptional, but not a priori necessary. Logics are exceptional because they can neither be demonstrated as valid nor be confirmed by observation without entering a circle, and their motivation based on intuition is unreliable. On the other hand, logics do not express a priori necessities of thinking because alternative non-classical logics have been developed. Section 2 reflects the controversies about four major kinds of non-classical logics—multi-valued, intuitionistic, paraconsistent and quantum logics. Its purpose is to show that there is no particular domain or reason that demands the use of a non-classical logic; the particular reasons given for the non-classical logic can also be handled within classical logic. The result of Sect. 2 is substantiated in Sect. 3, where it is shown (referring to other work) that all four kinds of non-classical logics can be translated into classical logic in a meaning-preserving way. Based on this fact a justification of classical logic is developed in Sect. 4 that is based on its representational optimality. It is pointed out that not many but a few non-classical logics can be likewise representationally optimal. However, the situation is not symmetric: classical logic has ceteris paribus advantages as a unifying metalogic, while non-classical logics can have local simplicity advantages.

1 The problems of justifying a system of logic

1.1 Apriori reasons for logic operations and the classical-non-classical controversy

According to the traditional view, the truth or validity of the rules of logic can be justified by a priori reasons. To a certain extent, this seems indeed to be the case, if we consider the logical operators as necessary structural means for the possibility of describing arbitrary 'manifolds' or 'worlds. In this perspective, the logical operations can be justified in 'transcendental way' in the sense of Kant or of Wittgenstein's Tractatus (1921):

• (i) The possibility of a correct (true) description of any manifold presupposes the operation of conjunction, by which we can represent complex facts having several components.

• (ii) Describing a manifold (world) consists not only in saying what is the case, but also in saying what is not the case, i.e., which descriptions are incorrect (false). This presupposes the operation of negation.

• (iii) Descriptions may be incomplete, in which case they can only say that one of several possible descriptions is correct. This requires the operation of disjunction. Moreover, expressing that the correctness of one description allows to infer the correctness of another description requires the operation of implication.

• (iv) If we enrich the operations of conjunction and disjunction by the idea of infinity, we obtain the universal quantifier (as an infinite conjunction) and existential quantifier (as an infinite disjunction).

However, these a priori reasons for the logical operations of propositional and predicate logic do not determine the precise meaning and logical rules of these operations. They constitute necessary conditions, but are too weak to justify a system of logic. The so-called classical logic is characterized by an additional semantic principle, the principle of bivalence: every statement p that is expressed in a semantically complete (non-indexical) way is either true or false. Thus, p can not be 'undetermined', i.e. neither true nor false (the principle of excluded middle), nor can p be 'dialethic', i.e. both true and false (the principle of non-contradiction). It should be emphasized that the principle of bivalence is not meant in an epistemic but in an ontological sense. Ultimately this principle expresses the determinateness of reality: if "p" is a semantically complete (non-indexical) sentence, then either p or not p must obtain.

Most non-classical logics reject the principle of bivalence, but for different reasons. In this paper we will consider four kinds of non-classical logics: (i) three-valued logic and their generalizations to many-valued logics, (ii) intuitionistic logic, (iii) paraconsistent logic and (iv) quantum logic. Lukasiewicz' three-valued logic (Łukasiewicz, 1920) was motivated by the argument that there are sentences whose truth value is objectively undetermined, with the consequence that the classical law of the excluded middle (p ∨ ¬P) becomes invalid. Brouwer's intuitionistic logic (Brouwer, 1912) originated in the domain of mathematics and was motivated by the replacement of the Platonist notion of mathematical truth by the concept of constructive mathematical verification, with the result that the classical law of double negation (¬¬p → p) becomes invalid. Paraconsistent logic was motivated by the attempt to avoid the irrelevant inference of 'explosion' (p ∧ ¬p / q) by assuming that statements can be both true and false (Priest, 2006). Still different is the rationale of quantum logic that introduces a non-classical disjunction operation violating the expansion direction of distribution, p ∧ (q ∨ r) → (p ∧ q) ∨ (p ∧ r) (Birkhoff & von Neumann, 1936).

The plan of this paper is as follows. In Sect. 1 we discuss the problems of justifying a system of logic from a general epistemological viewpoint. The key problem is that for assessing the adequacy and the relative merits of a system of logic one would need external standards, but apparently there are no such external standards. Attempts of justifying a logic by demonstration or observation end up in circular reasoning, and the justification of logical rules based on intuition is unreliable. In Sect. 2 we analyze the philosophical controversies about four major kinds of non-classical logics and show that in every case the particular reasons given for the non-classical logic can also be handled within classical logic. This result will be substantiated in Sect. 3, where it is shown (referring to other work) that non-classical logics can be translated into classical logic in a meaning-preserving way. Based on this fact we propose a justification of classical logic that is based on its representational optimality. In the last part the paper (Sect. 4) it turns out that not many but a few non-classical logics are likewise representationally optimal. Nevertheless the situation is not symmetric, since classical logic has important ceteris paribus advantages as a unifying metalogic.

1.2 Exceptionality without aprioricity

In contemporary philosophy of logic the view of logical anti-exceptionalism has been developed, as an opposition to the traditional logical apriorism. Proponents of anti-exceptionalism (e.g., Bueno, 2010; Hjortland, 2017; Priest, 2006; Williamson, 2014) argue that logics are not 'exceptional' compared to the empirical sciences. More precisely, they claim that (a) it is false that the laws of logic have an exceptional status of a priori necessities, as it was traditionally assumed in philosophy; rather (b) systems of logics have to be supported or revised based on empirical facts, similar as this has been the case for physical geometries (cf. Putnam, 1974, p. 55). We argue that thesis (a) is right, but thesis (b) is not tenable. The situation in logic is very different from the case of geometry. The justification of different systems of physical geometry (say Euclidean versus non-Euclidean) is based on independent logico-mathematical description systems that do not presuppose a particular geometry. But every description of evidence for or against a given logic L presupposes a metalogic for describing this evidence and drawing conclusions from it about the status of L (cf. Sereni & Sforza Fogliani, 2020; Woods, 2019). In the next three sections we describe in detail how attempts to demonstrate the validity of logic by semantic proofs, by observation or by intuition end up insuperable difficulties. For purposes of logical formalization we use p₁, p₂, …, q, r… for (propositional) variables, A, B, … for arbitrary formulas and Γ, Δ, … for arbitrary sets of formulas; ¬, ∧ , ∨ and → denote classical negation, conjunction, inclusive disjunction and material implication, respectively; |== denotes logical consequence and |— logical derivability.

1.3 Circularity of demonstrations of validity

It is well-known to logicians that in order to prove a logical rule as semantically valid one has to assume this rule (or related rules) in the metalogic (cf. Haack, 1976). In epistemological movements such as coherentism and (partly) externalism such rule-circular justifications (as they are called) are considered as epistemically virtuous.¹ It can be demonstrated, however, that rule-circular justifications are epistemically worthless, because with their help both a rule and the opposite rule can be proved. For example, Salmon (1957) has shown that both the rule of induction and that of counter-induction can be rule-circularly 'justified' as follows:

Rule-circular 'justification' of induction: Past inductions have been successful. Therefore, by the rule of induction: Future inductions will be successful.

Rule-circular 'justification' of counter-induction: Past counter-inductions have not been successful. Therefore, by the rule of counter-induction: Future counter-inductions will be successful.

Similar examples can be given in the domain of meta-logical validity proofs (cf. Haack, 1976, p. 115). For example, not only Modus Ponens (MP: A, A → B / B) but also the opposite rule, that we call 'Modus Nonsense' (MN: A, A → B / ¬B), can be rule-circularly 'proved' as follows:

Rule-circular proof of the validity of Modus ponens: 1. Premise: True(A), 2. Premise: True(A → B), 3. True(A) → True(B) from 2 by the truth-table for →, 4. True(B) from 1 and 3 by MP.

Rule-circular proof of the validity of Modus nonsense: Steps 1, 2, 3 as above. Continue as follows: 4*. ¬True(B) from 1, 3 by MN, 5*. True(¬B) from 4* by the truth-table for ¬.

Rule-circular validity proofs may be semantically illuminating, but they do not provide real justification. Rather, the validity or invalidity of these rules is assumed as basic 'knowledge' that is simply accepted. Technically this basic knowledge can be explicated either semantically, in propositional logic by means of truth tables, or syntactically by means of an axiomatic system. In our example, we 'know' that only step 4 but not step 4* is correct, because only the rule MP but not the rule MN is validated by the classical truth tables, that are assumed as basic.

1.4 Circularity of observational evidence for logics

Can the validity of logical rules be confirmed by empirical evidence, as anti-exceptionalists claim? There are two kinds of empirical evidence: (i) observational evidence, that will be considered in this section, and (ii) evidence by intuition, that is treated in the next section.

Let Fa stand for an atomic proposition, short for "a has the property F", and O(Fa) stand for "it has been observed that a is F". We assume that F is an observable predicate and a refers to an observable individual or spacetime region.² Our crucial question is: what does it mean to observe a logically compound proposition? This is intricate, because logical connectives carry structural information that is not itself the object of observation.

First consider a negated observation statement, say "this jacket has no stripes", abbreviated as ¬Fa. The not-being of something is not directly observed; it manifests itself in not observing something during careful observation. Observing that this jacket has no stripes means that after visually scanning all of this jacket's surface (under normal conditions of vision), no stripes on this jacket have been seen. More generally, that ¬Fa has been 'observed' (or is justified by observation) means plausibly that Fa has not been observed, together with an 'observational completeness' condition asserting that "all relevant parts of a have been observed", abbreviated as O(all-of-a). In formulas, O(¬Aa) ↔ ¬O(Aa) ∧ O(all-of-a), where Ax may be a simple or complex predicate. Now let us ask: can we test by observation whether the law of double negation, ¬¬Fa → Fa, is valid? According to our analysis, O(¬¬Fa) ↔ ¬O(¬Fa) ∧ O(all-of-a) ↔ (¬¬OFa ∨ ¬O(all-of-a)) ∧ O(all-of-a) ↔ ¬¬O(Fa) ∧ O(all-of-a). Thus, that ¬¬Fa has been 'observed' means that it is not the case that Fa has not been observed, together with the completeness condition O(all-of-a). Now, is it possible to refute the classical law of double negation, ¬¬Fa → Fa? Refuting this law would mean not having not observed that Fa and at the same time not having observed that Fa, i.e., ¬¬O(Fa) and ¬O(Fa), together with O(all-of-a). But given that we describe the observational facts within classical logic, this is impossible, because ¬¬O(Fa) entails O(Fa) by the law of double negation, which is in turn a straightforward consequence of bivalence: either Fa was observed, or Fa was not observed. In conclusion, if someone asserts ¬¬O(Fa) and ¬O(Fa), then (s)he either makes an inconsistent assertion or uses a different non-classical negation. We are as wise as before: the result of an 'observational test' of the law of double negation depends whether we describe the observations using classical versus intuitionistic negation. If we use classical negation, a negative test outcome is impossible, but if we use intuitionistic negation, we are no longer testing classical negation.

A similar situation arises for the conjunction of observations: observing Fa ∧ Ga, e.g., that this jacket has white stripes and red spots, means that both conjunctive components Fa and Ga are observed: O(Fa ∧ Ga) ↔ (OFa ∧ OGa). Can the law of simplification, (p ∧ q) → p, be put under observational test? To possess observational evidence against this law would mean that O(Fa) ∧ O(Ga) hold true and ¬O(Fa) holds true. However, assuming classical logic this situation is impossible, since O(Fa) ∧ O(Ga) entails O(Fa) by the law of simplification. If someone asserts O(Fa) ∧ O(Ga) and ¬O(Fa), then s(he) either makes an inconsistent assertion or uses a different non-classical conjunction. Similar stories may be told about attempts of testing the classical laws of disjunction (or material implication). In conclusion, observational 'tests' of a logic L end up in a circle: if L is used in the metalogic, their outcome must be positive, and if not, they fail to test L.

1.5 Unreliability of intuitive evidence for logics

The objections against observational evidence in the previous section cannot be raised against intuition, because also logically complex propositions may be the immediate content of an intuition. For example, a person may have the intuition that ¬¬p, but not have the intuition that p. Is it reasonable to count this as evidence against the validity of the law of double negation?

For many philosophers intuitions serve as basic justifiers of philosophical principles. For Priest (2016, p. 355) the data on which logics should be based are human intuitions about the validity of statements or inferences. Similar arguments have been proposed in cognitive science (Cohen, 1981). The major objection against this position is that humans intuitions are unreliable (cf. Cappelen, 2012). Before we elaborate this objection we have to clarify the notion of intuition that we criticize.

Sometimes all sorts of inner experiences are subsumed under 'intuition', but here an important distinction is necessary. As long as the content of 'intuitions' are expressed in the subjective mode, they reflect introspective experiences, such as "it appears to me that Euclidean geometry is necessary". These sort of intuitions express unproblematic introspective propositions about the contents of one's own consciousness. For a critical foundation-theoretic epistemology, the transition from introspective facts to beliefs about external facts of the world corresponds to an inference, that is often unjustified and can be abductively justified only under certain conditions (Schurz, 2021a). In contrast, intuition-based philosophy takes intuitions as direct evidence for objective truths: here the fact that certain people (philosophers) or many people (common-sense) have certain intuitions (e.g. that Euclidean geometry is necessary) is taken as direct evidence for the truth of the intuited propositions. This is the sort of intuition that we criticize.

Many cognitive studies show that people's intuitive reasoning of people is incorrect, starting with the famous card selection task of Wason (1959) that tested people's reasoning with implications. Priest (2016, p. 355) argues that the mistakes untrained adults make in Wason's selection task go away if one explains the errors to them, but this view is largely refuted by the statistical evidence (cf. Evans, 1982, ch. 8–9). Similar violations of valid rules were found in the domain of probabilistic reasoning (Kahneman & Tversky, 1972). These findings led many cognitive psychologists towards a general skepticism in regard to 'normative' status of logical and probabilistic rules of reasoning. Cohen (1981, p. 330) even argued that if people's reasoning deviates from these rules, this merely means that they have different intuitions about correct reasoning than logicians or probability theorists (for a critique cf. Schurz & Hertwig, 2019). Similar objections against intuition-based philosophy have been developed in the field of experimental philosophy, in which philosophical intuitions of test persons are tested empirically (cf. Weinberg et al., 2008, pp. 24–26).

In conclusion, it is highly problematic to justify the correctness of logical rules by intuitions. Moreover, the understanding of logical rules of test persons is highly content-specific (Evans, 1982, p. 105ff.), which violates the fundamental logical rule of uniform substitution. If rules of logic were justified by average human intuitions, not much of logic, whether classical or non-classical, would be left over. On the other hand, if with intuitions only the intuition's of particular philosophers are meant, the intuition-based account would become dogmatic, and if only 'correct' intuitions are meant, it would become circular.

1.6 The threats of incommensurability and subjectivity

So far we could not find a functioning strategy for justifying a system of logic; the discussed justification attempts ended up either in circularity or in subjective arbitrariness. This result (if it stays that way) seems to speak in favor of the exceptional status of logic as irreducibly basic. In combination with the plurality of (classical or non-classical) logics this exceptional feature becomes highly problematic. There are two threats emerging from this situation. First, the threat of relativism: It appears to be largely a subjective matter which logic one chooses, based on subjective intuition or taste, but not upon objective or intersubjective reason. The threat of relativism would not be so bad if the choice of a logic were largely a matter of convention, like the choice of a conventional terminology. But the opposite seems to be the case: logic constitutes the innermost core of our belief system, determining all other parts. This brings us to the second threat—that of incommensurability: Proponents of different logics appear to be in a fundamental disagreement that cannot even be formulated in a neutral way, because every formulation presupposes the adoption of a logic.

1.7 Justification of logic by means of representational usefulness

One method of justifying a logic has not been refuted so far: its 'pragmatic' justification by its usefulness in regard to given epistemic purposes, prominently represented, for example, by Carnap (1939). One major purpose of a system of logic is the explication of correct inference. The justification of a system of logic by the usefulness of correct inferences is not of much help, because what 'correctness' means depends on the logical system. Beyond correctness, inferential usefulness concerns more the question of proof-theoretical calculi than that of logics in the philosophical sense. However, explicating correct inference is only the prima facie purpose of logics. The rules of correct inference depend themselves on the semantic principles characterizing the underlying logical operators. As argued in Sect. 1.1, logical operators are necessary structural means for representing arbitrary 'manifolds' or 'worlds. The deepest purpose of a logical system is that of representation. Thus, we propose that systems of logics should be justified by their representational usefulness.

Proponents of non-classical logic often justify their preferred logic by its representational usefulness for a particular domain (cf. Bueno, 2010, p. 108, p. 115). However, these pragmatic justifications are only plausibility arguments and never 'mandatory. The next section contains a tour through the controversies about the major kinds of non-classical logics. Its purpose is to show that the particular reasons given for a non-classical logic can always be handled within classical logic, and whether their handling in one or the other logic is the simpler strategy depends on the details of the domain. Beyond this result, our foray through the classical-non-classical controversies will show that their participants, though being proponents of different logics, have no problems in exchanging rational arguments. As we shall see, this is possible since non-classical structures can be represented also within classical logics.

2 Pros and cons of non-classical logics in relation to classical logic

2.1 Three-valued and many-valued logics

Three-valued logic accepts the existence of an objective reality, but rejects the determinateness of its properties. Plausible but controversial reasons for this position come from the theory of vagueness (Sorensen, 2018). They are based on the fact that the meaning of many predicates of human languages is not completely fixed, but has vague boundaries. In reaction to this point the principle of determinateness can be defended by relativizing it to an ideal language, whose predicates are semantically completely specified. For example, one could define a strict borderline between “blue” and “green” based on physical wave lengths. Arguably, however, such an ideal language is not accessible to human beings, at least not in all domains. Therefore the ideal-language-relativized formulation the principle of determinateness loses a bit of its attractiveness. This constitutes one of the main motivations for development of three-valued and many-valued logics, starting with Lukasiewicz' trivalent logic (1920), L₃, with the truth values true, false and undetermined.

Later, different variants of three-valued logics have ben developed, and three-valued logic has been mathematically generalized to many-valued logics with arbitrarily many 'truth values', abstracting from a particular philosophical interpretation of the truth values (Malinowski, 1993). A multi-valued logic L in the generalized sense is semantically characterized by a set of (truth-)values Val and a subset Des ⊂ Val of designated (truth-)values. The triple <Val, Des, {t_c:c ∈ C} > (with {t_c:c ∈ C} being the set of generalized truth-tables for a set of connectives C) is called a Val-valued logical matrix. A formula A is defined as logically true if all possible valuations of the propositional atoms of L's language assign to A a designated value.

Vagueness constitutes a major argument for the development of three-valued logics, but not the only one. An even stronger argument for the indeterminateness of microphysical reality comes from quantum physics. Remarkably, however, orthodox quantum logic does not give up semantic bivalence, but the law of distribution (see Sect. 2.4). In any case, the philosophical controversy over the ontological foundations of three-valued logics centers around the question whether there are objectively undetermined states in certain regions of our world or not. This formulation gives us the clue how we can express three-valued assertions in two-valued logics. Even if a sentence p is objectively undetermined, the statement that p is objectively undetermined is two-valued, either true or false, but certainly not undetermined—no proponent of a three-valued could argue that way, because assuming a trivalent semantic assignment just means that these statements are bivalent. More generally, statements about the truth value of many-valued propositions are strictly bivalent. This observation gives us the basic instruction for the translation of many-valued logics into bivalent logic described in Sect. 4.1.³

2.2 Intuitionistic logic

Brouwer's intuitionistic logic L_int is based on the rejection of mathematical Platonism. According to the anti-Platonist position, mathematical objects (such a numbers) do not have a mind-independent existence, but are cognitive constructions. Therefore the classical notion of truth is replaced by the concept of mathematical verification. A mathematical verification of a statement p consists in a constructive proof with conclusion p, and a mathematical falsification in a constructive proof from assumption p to a contradiction q ∧ ¬q. Since by the results of Gödel and Church there exist mathematical propositions whose truth value is undecidable, the verificationist view has the consequence that several laws of classical logic are no longer valid, foremost the laws double negation (¬¬p → p) and that of excluded middle (p ∨ ¬p).

These consequences come at a high price. Standard mathematics is based on classical logic, and only a certain part of standard mathematics can be 'saved' within intuitionistic logic. For example, transfinite induction over well-ordered classes, needed for proofs in mathematical analysis, requires the set-theoretic axiom of choice. This axiom is not accepted in intuitionistic or constructive logic (Bridges & Palmgren, 2018, Sect. 4). Moreover, standard completeness proofs of logics, including the completeness proof for intuitionistic predicate logic, rest on 'Gödel's lemma' (if every L-consistent formula set Δ has a model, then Γ |==_L A implies Γ |—_L A), whose proof requires the law of double negation, while intuitionistically only Γ |==_L A implies Γ |—_L ¬¬A can be derived. Kreisel (1958) showed that there is no purely intuitionistic completeness proof for intuitionistic predicate logic.

In the domain of factual science, the replacement of classical by intuitionistic logic is even more controversial. Here this replacement amounts to a strong version of metaphysical anti-realism, that has been endorsed, for example, by coherentists (Blanshard, 1939) or by verificationists (Dummett, 1991).

On the other hand, let us assume that one really rejects the assumption of an objective reality for the domain that one describes. Then the semantics of bivalent logic can only be regarded as an idealization that is epistemically useful, but does not correspond to a structure of reality. This may be considered as a reason strong enough to reject the constructively invalid part of mathematics. However, even this step is not enforcing. Compare the situation with imaginary numbers in mathematics: They have no counterpart in reality and yet they are useful for describing physical objects.

However that may be, more important for us is the following point. The meaning of assertions of classical logic is based on the

• (1) Truth view of assertion: Asserting p means that the truth of p is asserted.

This view does not only apply to bivalent logics, but to all many-valued logics that have "true" as their designated value. In a slight generalization, many-valued logics with several designated values subscribe to the

• (2) Designated-value view of assertion: Asserting p means asserting that p has a designated value.

The philosophical characteristics of intuitionistic logic is that it replaces the truth view of assertion by the following.

• (3) Proof view of assertion: Asserting p means asserting that p has a constructive proof.

The 'logic of mathematical verification' need not be set in opposition to classical logic. It may also be described within classical logic, by making provability claims explicit. For provability assertions the principle of bivalence holds again, i.e., for every p either Provable(p) or ¬Provable(p) holds; most proponents of L_int would agree with this. What is only denied is that for every p, Provable(p) or Provable(¬p) holds. The proponent of classical logic agrees with this, but expresses it by means of an explicit proof operator, instead of switching from the truth view to the proof view of assertion. In conclusion, we found a perfect way of expressing intuitionistic logic within classical logic that will be worked out in Sect. 3.2.

2.3 Paraconsistent Logic

Paraconsistent logic has two major motivations: relevance and antinomies. We first discuss relevance. Following from the definition of a valid inference, classical logic admits valid inferences without any relevant connection between premises and conclusion; first and foremost the (in)famous inference

• (4) (EFQ, ex falso quodlibet): A, ¬A / B (for arbitrary formulas A, B).

(EFQ) is also called explosion, since it allows to infer from a contradiction every proposition whatsoever. Connected with it is the 'material' version of EFQ:

• (5) (mEFQ): ¬A → (A → B).

Relevance logic attempts to block these two irrelevant inferences and implications, but maintain standard logical properties such as transitivity and closure under substitution (Anderson und Belnap, 1975). It turned out, however, that this is only possibly by severe restrictions of classically valid inferences. For example, disjunctive syllogism (DS): A ∨ B, ¬A / B has to be rejected altogether and conjunction introduction (Con) A, B / A ∧ B has to be restricted, although both inferences are highly plausible (Schurz, 1999; Williamson, 2014). Moreover, there is no unique solution to the problem; a variety of different relevance logics has been developed. One possibility to obtain a relevance logic is paraconsistent logic in which a proposition can be both true and false (Priest, 1979, 2006; Priest et al., 2018, Sect. 3.7).

There is, however, also a classical account to relevant inference that is inspired by linguistic and cognitive approaches to relevance (starting with Grice, 1975). In this account irrelevant inferences are not considered as invalid, but validity and relevance are treated as separate properties of inferences. Relevance criteria such as the salva validitate replacement criterion (Schurz, 1991; Weingartner, 2000) or the content criterion (Gemes, 1994) are imposed as a filter on classically valid inferences, separating the relevant from the irrelevant ones. For example, (EFQ) A ∧ ¬A |== B is irrelevant because B can be replaced by any arbitrary formula (also by ¬B), salva validitate of the inference, i.e., the inference remains valid after this replacement. Note that in the latter account, DS is relevant but Add(ition) (A/A ∨ B) is irrelevant, while for relevance logic, DS is invalid but Add is valid (Schurz, 1999).

The second motivation of paraconsistent logic comes from the existence of antinomic sentences (Priest, 2006), such as the Liar sentence ("I am false") or Russell's antinomy. Antinomic sentences can be constructed within a self-referential language ${\mathcal{L}}_{{\text{T}}}$ that extends ordinary 1st order language by a truth predicate "T(rue)", together with a recursive name-function n mapping formulas A of ${\mathcal{L}}_{{\text{T}}}$ uniquely into names of ${\mathcal{L}}_{{\text{T}}}$. The liar antinomy proves that within classical logic, Tarski's explication of the correspondence theory of truth—True(n(A)) iff A, for all A ∈ ${\mathcal{L}}_{{\text{T}}}$—leads to an inconsistency. Standardly this is regarded as a deep insight about the diagonalization power of self-referential languages. From the perspective of paraconsistent logic, the insight doesn't follow, because the inconsistency of a system is not a reason to reject the system. Paraconsistent logicians argue that this has the advantage that a restriction of Tarski's truth schema and of the naive comprehension schema of set theory becomes unnecessary. Unsurprisingly, the paraconsistent position is highly controversial. For example, Williamson (2017) argues that the classical solution of the liar antinomy that restricts Tarski's truth schema is more adequate than the paraconsistent rejection of the law of non-contradiction, because Tarski's disquotational truth schema expresses a much less fundamental matter than the law of non-contradiction.

Not all but many paraconsistent logics can be characterized by means of finite truth value matrices (Priest et al., 2018, Sect. 3.6). The simplest paraconsistent logic is the logic LP ("logic of paradox") developed by Priest (1979). It is a species of a three-valued logic, having instead of the third value "undetermined" the value "both true and false", abbreviated as b (or "p" for "paradoxical", as in Priest, 1979). The values "t" and "f" now mean "true only" and "false only", respectively. The truth-tables of LP are that of Kleene's trivalent logic; they are as in L₃ except that they have b → b = b instead of u → u = t. The more important difference of LP compared to L₃ is that LP considers both values t and b as designated. As a result of this step, LP's logical theorems are identical with the theorems of classical logic, but many classically valid inferences become invalid. For example, (EFQ) p ∧ ¬p |== q is invalid, as intended, since there are valuations assigning b to p and thus to p ∧ ¬p, but f to q. Unfortunately, also some highly reasonable classically valid rules become LP-invalid, for example (MP) p, p → q / q and (Trans→): p → q, q → r / p → r (Priest, 1979, p. 228).

More importantly, paraconsistent statements don't seem to convey clear information. For example, if one assumes a paraconsistent metalogic, then arithmetics is not simply consistent or complete; it is both incomplete and complete, consistent and inconsistent. These consequences seem absurd (cf. Denyer, 1995), but if one really assumes that there are arithmetical propositions that are both true and false, they seem to be unavoidable and Priest's observations are only consequent. However that may be, the important point for us is, again, that the controversy about the possibility of sentences that are both true and false can be carried out within classical logic. The observation made in Sect. 3.1 applies similarly to paraconsistent logics: the statements True-only(p), False-only(p) and Both(p) are again bivalent, either true or false but not both.⁴ This gives us the basic strategy of embedding paraconsistent logic in classical logic, elaborated in Sect. 3.3.

2.4 Quantum Logic

Anti-exceptionalists frequently assume that the non-classical structure of quantum events is an uncontroversial fact. In contrast to this opinion we show in this section that especially in the quantum domain it is controversial whether quantum or classical logic provides the more adequate reconstruction of the structure of quantum events.

Quantum logic intends to explicate the structure of 'experimental' propositions about quantum-physical systems, having the form "the magnitude m of system x has value v", in short "m(x) = v" (van Fraassen, 1975). For example, m(x) can be the (real-valued) position or the (discrete-valued) spin of an electron x. The system x is described by its physical state or wave-function ψ(x). The set of all possible wave functions ψ_i(x) of x is called the 'Hilbert space' Σ(x) (which is a set of wave functions viewed as vectors and closed under linear combinations). Each magnitude m corresponds to a mathematical operator M describing m's measurement. M's application to ψ(x) determines the value of m(x)

• either sharply, in which case ψ(x) is a pure state w.r.t. the magnitude m and m is an 'eigenvalue' of M, i.e., Mψ(x) = m·ψ(x) holds,

• or merely probabilistically, in which case ψ(x) is a so-called superposition (or 'entangled') state w.r.t. m, meaning that ψ is a linear combination of two or more pure states w.r.t. m. In this case, a measurement of m changes the systems's state from a superposition state to a pure state for one of the possible values of m according to a probability distribution P (computed by P(m(x) ∈ Δ) = ∫_r∈Δψ*Mψdr). This measurement-induced change is called the collapse of the wave function.

Importantly, certain pairs of quantum-physical magnitudes cannot simultaneously have a sharp value. For example, according to Heisenberg's uncertainty relation it is impossible that both the position s and the momentum p can be sharply realized; it rather holds that Δs⋅Δp ≥ h/2π. Thus if ψ(x) is a pure state w.r.t. p, it is a superposition state w.r.t. s. Similar 'incommensurability' relations hold between other pairs of magnitudes (e.g., for the spin in x- and z-direction).

Although this interpretation of quantum physics implies a revision of the metaphysics of classical particle realism, it is microphysically plausible. According to the standard wave-particle dualism, a micro-object may behave (i) as a wave or (ii) as a particle, depending on the situation; in case (i) its position is unsharp and in case (ii) its momentum (corresponding to wave-length) is unsharp. Admittedly some deep problems of quantum measurement remain unsolved, but among all interpretations of quantum physics (Myrvold, 2018), this interpretation is most broadly accepted. It does not motivate a non-classical logic, but merely a revision of the classical metaphysics.

In contrast, quantum logic favors a different (meta-)physical view. It is the crucial feature of the standard version of quantum logic (QL) going back to Birkhoff and Neumann (1936) that the superposition state of a system is expressed as a non-classical disjunction (∨_q) of pure states. For example, if an electron in a two-slit experiment is in a superposition of the two possible positions states s_r (going though the right slit) and s_l (going to the left slit), then QL describes this state as s_r ∨_q s_l. If one has classical disjunction in mind, this representation of superposed states is clearly wrong. It is a core insight of quantum physics that the identification of a superposed state with a (classical) disjunction of 'hidden' pure states leads to wrong predictions (as demonstrated in the famous 'no-hidden-variables' theorems; Bell, 1966). Therefore already early critics of QL objected that a superposition state is genuinely different from a disjunction of pure states (Popper, 1968, p. 685; Gardner, 1972, p. 523). The defenders of QL replied that quantum disjunction is different from classical disjunction (∨) and that the description of superposition states by non-classical disjunctions has certain advantages to be discussed in the following.

Indeed, quantum-logical disjunction is radically different from classical disjunction. Assume that the electron in the two-slit experiment is in the superposition state s_r ∨_q s_l w.r.t. position and in the pure state p w.r.t. momentum. Then QL describes this situation as p ∧ (s_r ∨_q s_l), but by the incommensurability of momentum and position, both conjunctions p ∧ s_r and p ∧ s_l are false. Thus the expansion direction of the classical law of distribution, (D_e): p ∧ (q ∨ r) → (p ∧ q) ∨ (p ∧ r), is invalid according to QL. Putnam argued that the failure of (D_e) would allow for a fully realistic interpretation of quantum physics, because within QL we can say that the electron is always in a definite position and momentum state. Measurement doesn't bring sharp values 'into being' and classical realism is retained; the only mistake is accepting the law of distribution (Putnam, 1968, p. 186; 1974, p. 57). However, as several authors (e.g., Dummett, 1976; Stachel, 1986) pointed out, this argument is flawed. To see this we must simply observe that although the quantum-logical disjunction s_r ∨_q s_l is true in the superposed state, both disjuncts of the disjunction are false (van Fraassen, 1975, p. 584; Dalla Chiara & Giuntini, 2002, p. 133). This fact also explains why the semantics of QL is bivalent: in the superposed state the propositions s_r and s_l are not undetermined, as in Reichenbach's three-valued quantum logic (Reichenbach, 1944), but false; however, this not expressible in QL since classical negation ¬ is not available.

To explain this point from another angle, the assertion "m(x) = r" does not merely mean in QL that the value of magnitude m for system x has actually been measured as r (this could not be uniquely related to x's state), but that the measurement of m will produce the value r with certainty, i.e., x is in a pure state w.r.t. m (Dalla Chiara & Giuntini, 2002, p. 131). Likewise the proposition "m(x) = r₁ ∨_q m(x) = r₂" means that with certainty the measurement of m will produce one of the outcomes r₁ or r₂—which is also true if x is in a superposition state w.r.t. m. So, two intensional operators are involved in QL assertions: "with certainty" (C) and "is measured" (M). Thus we may say that in QL the truth-view of assertion is replaced by the

• (6) Measurement-with-certainty view of assertion: Asserting p means that with certainty measurement will verify p.

Let p_i abbreviate the quantum-logical proposition m(x) = r_i. Then the explicit meaning of p_i is CMp_i and the explicit meaning of p₁ ∨_q p₂ is C(Mp₁ ∨ Mp₂). Of course, C(Mp₁ ∨ Mp₂) is different from the classical disjunction CMp₁ ∨ CMp₂. We thus have found a possibility for expressing formulas of QL within classical logic that will be formally treated in Sect. 3.4.

We have seen that QL-'disjunction' ∨_q is substantially different from classical disjunction. The reason why many QL-laws—all except of (D_exp)—resemble the laws of L₂ is that QL introduces a corresponding quantum-logical negation ¬_q that is likewise substantially different from classical negation ¬, but fits with ∨_q in similar ways as ¬ fits with ∨. Let the extension ||A|| ⊆  Σ of a quantum proposition A be defined as the set of states in Σ verifying A (with certainty). Then ||¬_qA|| is defined as the set of all states that are orthogonal to all states verifying A (where two state vectors α, β are orthogonal iff their scalar product is zero). ||¬_qA|| is a proper subset of the extension Σ − ||A|| of classical negation, while ||(A ∨_q B)|| is a proper superset of the extension ||A|| ∪ ||B|| of classical disjunction. Only the QL-extension of conjunction ∧ is the classical intersection, ||A ∧ B|| = ||A|| ∩ ||B||. It follows from these definitions is that the extensions of QL-propositions are always closed under linear combinations.

Most contemporary quantum logicians agree that QL doesn't solve the metaphysical problems of quantum physics (Bacciagaluppi, 2008). An alternative and in fact earlier justification of QL was based on an empiricistic viewpoint, according to which the states of quantum systems should be solely described in terms of measurement results of the form m(x) = r (Birkhoff & Neumann, 1936; van Fraassen, 1975, p. 578). This justification is problematic for two reasons:

First, as we have seen, an 'experimental proposition' m(x) = r asserts more than an actual measurement result. It asserts that the measurement result will obtain with certainty, but "certainly(p ∨ q)" is different from "certainly p or certainly q".

Second and more generally, it is broadly accepted in contemporary philosophy of science that scientific theories contain theoretical concepts or laws that are not directly observable or confirmable by observation. Many theoretical properties that are essential to quantum-physical systems do not express measurement results and, thus, cannot be expressed in QL—for example that a system x is not in a particular pure state (which requires classical negation) or that x is in a proper superposition state (cf. Baltag & Smets, 2011, p. 292).

Because of these differences, it is broadly agreed that QL cannot replace classical logic: classical logic is needed to express the full structure and consequences of quantum physics (Baltag & Smets, 2011; Stachel, 1986). On the other hand, quantum logic can express physical operations (e.g., linear combinations) that go beyond what classical logic can express. What is needed is a unified system containing the resources of both classical and quantum logic, which is possible by embedding QL into classical logic (see Sect. 3.4).

3 Translations of non-classical logics into classical logic

In the previous section we have seen that all non-classical logics introduce additional semantic parameters that are not explicitly expressed in the syntax. Many-valued logics introduce additional truth values, intuitionistic logic introduces assertions of provability and quantum logic assertions about measurement results occurring with certainty. Our proposed method of translating a non-classical logic into an extension of classical logic makes these parameters explicit by adding intensional operators to the language of classical logic. Based on this method a non-classical logic can be translated into an extended classical logic, via additional axioms for these operators that mirror the axioms of the non-classical logic.

The study of translations methods between different logics has become an area of increasing research (Carnielli et al., 2009). The epistemologically important feature of the translation method proposed by us that distinguishes it from many other translation methods in the literature is that it preserves meaning. In this section we explain the major results of this translation method whose technical proofs are described elsewhere. Concerning formalization, we use indexed letters L_i for systems of propositional logics and ${\mathcal{L}}_{{\text{i}}}$ for their languages, identified with the set of their well-formed formulas. L₂ denotes the classical (bivalent) propositional logic and Γ |==_L2 A stands for the corresponding inference relation (defined via truth preservation).

3.1 Translating three-valued and many-valued logics

We start with Lukasiewicz three-valued logic L₃. Its language, ${\mathcal{L}}_{{3}}$, has four basic truth-functional connectives ¬, ∨, ∧ and →, where the three-valued conditional → is not definable in terms of the other three connectives. The truth values of L₃ are t³ (true), u³ (undetermined) and f³ (false). We use upper indices to distinguish trivalent truth values from bivalent ones, t² and f². Val₃ is the set of all possible trivalent valuation functions v³: ${\mathcal{P}}$ → {t³, u³, f³} over the set ${\mathcal{P}}$ of ${\mathcal{L}}_{{3}}$'s propositional atoms, recursively extended to arbitrary complex ${\mathcal{L}}_{{3}}$-formulas. (Likewise for Val₂ and v²: ${\mathcal{P}}$ → {t², f²}.)

It is convenient to represent the trivalent truth values f³, u³, t³ by the ranks − 1, 0, + 1. Based on this ranking, Lukasiewicz' three-valued truth-tables for the four connectives are described as follows:

• (7) v³(¬A) is the inverse of A's truth value,

  v³(A ∧ B) is the minimum of A's and B's truth value,

  v³(A ∨ B) is the maximum of A's and B's truth value, and

  v³(A → B) = equals t³/u³/f³ iff the rank difference v³(B) − v³(A) is not smaller than 0/− 1/− 2, respectively.

An ${\mathcal{L}}_{{3}}$-formula A is logically true in L₃, in short |==_L3 A iff v³(A) = t³ for all possible trivalent valuations v³ ∈ Val₃, and A follows from a formula set Γ in L₃, in short Γ |==_L3 A, iff all v³ ∈ Val₃ that make all formulas in Γ true make also A true.

Some theorems of L₃: p → (q → p), (¬q → ¬p) ↔ (p → q), (p ∨ q) ↔ ((p → q) → q).

Some non-theorems of L₃: p ∨ ¬p, ¬ (p ∧ ¬p), (p ∨ q) ↔ (¬p → q). Conditional proof fails for L₃.

The translation of L₃ into L₂ is based on the extension of ${\mathcal{L}}_{{2}}$ by three sentential operators T³, U³ and F³ expressing the trivalent truth value of their propositional argument. For p ∈ ${\mathcal{L}}_{{3}}$ the sentences T³p, U³p and F³p are bivalent and obey the obvious truth tables (values whose upper indices are omitted hold bivalently and trivalently):

• 

We don't need to introduce these operators in ${\mathcal{L}}_{{3}}$, because they are definable in L₃ as follows: U³(A) =_def (A ∨ ¬A) → (A ∧ ¬A), T³(A) =_def A ∧ ¬U³(A), and F³(A) =_def ¬A ∧ ¬U³(A) (the defining formulas are truth-functionally equivalent with their definienda). With help of these operators the three-valued truth-tables for the connectives can be mirrored as equivalence axioms of the extended bivalent language as follows:

• (8) For negation: T(¬A) ↔ F(A); U(¬A) ↔ U(A); F(¬A) ↔ T(A).

  For conjunction: T(A ∧ B) ↔ T(A) ∧ T(B); F(A ∧ B) ↔ F(A) ∨ F(B); U(A ∧ B) ↔ (U(A) ∧ ¬F(B)) ∨ ((U(B)) ∧ ¬F(A)).

  For the disjunction: T(A ∨ B) ↔ T(A) ∨ T(B); F(A ∨ B) ↔ F(A) ∧ F(B); U(A ∨ B) ↔ (U(A) ∧ ¬T(B)) ∨ (U(B)) ∧ ¬T(A)).

  For implication: T(A → B) ↔ F(A) ∨ (U(A) ∧ ¬F(B)) ∨ (T(A) ∧ T(B)); U(A → B) ↔ (T(A) ∧ U(B)) ∨ ((U(A) ∧ F(B)); F(A → B) ↔ T(A) ∧ F(B).

By adding the trivalent truth-value axiom, T(A) $\dot{\vee}$ U(A) $\dot{\vee}$ F(A) to (8) (with "$\dot{\vee}$" for exclusive disjunction) we obtain the axiom system Ax_Luk of Lukasiewicz' logic in the extended language ${\mathcal{L}}_{{{2}.{\text{Luk}}}}$ of classical logic.⁵

As explained in (1) of Sect. 2.2, our method of translating ${\mathcal{L}}_{{3}}$-assertions into ${\mathcal{L}}_{{{2}.{\text{Luk}}}}$-assertions is based on the truth view of assertion. Thus our translation function "τ_3→2" (from ${\mathcal{L}}_{{3}}$ into ${\mathcal{L}}_{{{2}.{\text{Luk}}}}$) is:

• (9) For all A ∈ ${\mathcal{L}}_{{3}}$: τ_3→2(A) = T³(A).

Examples (with upper and lower indices omitted; ‘≡’ for 'equivalent'): τ(p) = T(p), τ(¬p) = T(¬p) ≡ F(p), τ(p ∨ ¬p) = T(p ∨ ¬p) ≡ Tp ∨ Fp, τ(p ∧ ¬p) = T(p ∧ ¬p) ≡ Tp ∧ Fp, τ(p → q) = T(p → q) ≡ Fp ∨ (Up ∧ (Uq ∨ Tq)) ∨ (Tp ∧ Tq).

We use the same logical symbols for the two-valued and the three-valued propositional connectives (e.g., both "→" for two-valued and three-valued implication). This is not a problem, because whenever we translate an ${\mathcal{L}}_{{3}}$-formula into ${\mathcal{L}}_{{{2}.{\text{Luk}}}}$, the three-valued connectives are hedged in the scope of the intensional truth value operators T, U and F.

It can be shown that the translation (9) preserves the meaning of ${\mathcal{L}}_{{3}}$-formulas and L₃-logical truth and validity in the following sense (where L_2.Luk,τ is the subset of ${\mathcal{L}}_{{{2}.{\text{Luk}}}}$'s formulas that are Ax_Luk-equivalent with translations of ${\mathcal{L}}_{{3}}$-formulas):

• (10) Theorem (L₃ into L₂):

  1. For every v³ ∈ Val₃ there exists exactly one v² ∈ Val₂ over ${\mathcal{L}}_{{{2}.{\text{Luk}}}}$_,τ satisfying Ax_Luk such that for A ∈ ${\mathcal{L}}_{{3}}$: v³(A) = o iff v²(O(A)) = t², where O = T³/U³/F³ iff o = t³/u³/f³.

  2. (i) |==_L3 A iff Ax_Luk |==_L2 τ(A) (in words: A is L₃-logically true iff τ(A) is an L₂-consequence of Ax_Luk), and (ii) Γ |==_L3 A iff Ax_Luk ∪  τ(Γ) |==_L2 τ(A) (where τ(Γ) = _def {τ(B): B ∈ Γ}).

The proof of theorem (10) (see Schurz, 2021b, Sect. 3.1) rests on the fact that every ${\mathcal{L}}_{{2}}$-translation τ(A) of an ${\mathcal{L}}_{{3}}$-formula A in variables p₁, …, p_n can be equivalently transformed into a disjunction of conjunctions of modalized variables O₁p₁ ∧ … ∧ O_np_n (O_i ∈ {T³, U³, F³}) that mirrors A's trivalent truth table in L₂.

The proposed translation preserves meaning as well as possible. It is not literally possible to translate a trivalent atomic proposition p into a bivalent one, because in L₂ p has only two but in L₃ p has three truth values. What can be literally translated are the more fine-grained propositions T³p, U³p and F³p, whose meaning is strictly the same in L₃ and in L₂. This is sufficient for the translation of all assertions expressible in L₃, given the truth view of assertions. Moreover, by applying the Ax_Luk-equivalences the semantic composition of formulas of L₃ is fully reflected in L₂.

This meaning-preservation feature distinguishes the proposed translation account from many translation functions between logics studied in the literature (Carnielli et al., 2009). In these studies, translations are usually not accompanied by an extension of the (classical) language, at the cost that the translation functions do not preserve meaning; they only preserve the consequence operation. An example of translation functions that preserve neither meaning nor syntactic structure are the technically great translation functions of Jerábek (2012). An example of a non-meaning-preserving translation at the semantic level is the reduction of many-valued logics to bivalent logics proposed by Suszko (1977) (for details on both cf. Schurz, 2021b).

The truth value of T³(A) ∈ ${\mathcal{L}}_{{2}}$ depends only on the bivalent truth values of the modalized variables (O_ip_k), but not of the unmodalized variables (p_k). So far, the bivalent truth values of the modalized variables have not been related to the bivalent truth values of the unmodalized variables. For the semantic coherence between L₃ and L₂ we require the following

• (11) Bridge axioms: T³p → p and F³p → ¬p, for all p ∈ ${\mathcal{P}}$.

In words, a trivalently true (or false) atomic sentence is also bivalently true (or false, respectively), while for undetermined sentences their bivalent truth value is left open.

A similar translation strategy applies to all many-valued logics that are representable by means of finitely many truth values. For logics with several designated values one applies the designated-value view of assertion (see (2) and Sect. 2.3).

3.2 Translating intuitionistic logic

As explained in Sect. 2.2, in intuitionistic logic L_int the classical notions of truth and falsity are replaced by the concepts of mathematical verification and falsification. A well-known 'translation' of L_int into L₂ is based on Glivenko's double-negation theorem, but this translation does not preserve meaning, since p and ¬¬p mean different propositions in L_int. There is, however, another well-known translation of L_int into a modal extension of L₂, namely into the modal logic S4, that fits perfectly into our account of meaning-preserving translations. As explained in (3) of Sect. 2.2, intuitionistic logic is based on the provability view of assertion. So it is natural to translate the assertion that p in intuitionistic logic by □p, where the modal operator "□" is understood as constructive provability. As in the translation of many-valued logics, this translation gives us bivalence outside the provability operator: although □p ∨ □¬p is not L₂-true, □p ∨ ¬□p is again L₂-true. Constructive provability satisfies the laws of the modal logic S4, semantically characterized by the class of reflexive and transitive Kripke frames (W, R) (i.e., the accessibility relation R ⊆ W² between worlds is reflexive and transitive). The S4-axioms are (T): □A → A (what is provable is true, corresponding to reflexivity), (4): □A → □□A (provability of propositions is itself provable, corresponding to transitivity), and the axioms and rules satisfied by all Kripke frame logics, namely (K): □(p → q) → (□p → □q) and (N) |== A/|== □A. Based on this interpretation, the translation function from L_int into S4 is as follows; the informal interpretation of the translating condition is stated in brackets:

• (12) Translation (τ) from L_int to S4::

  For all p ∈ ${\mathcal{P}}$: τ(p) =  □p (p has a constructive proof.)

  τ(¬A) = □ ¬τ(A)  (Provably τ(A) leads to contradiction, i.e.,

  τ(A) cannot have a constructive proof.)

  τ(A ∧ B) = τ(A) ∧ τ(B)  (Both conjunctive components are provable.)

  τ(A ∨ B) = τ(A) ∨ τ(B)  (At least one disjunctive component is provable.)

  τ(A → B) =  □(τ(A) → τ(B)) (Provably every proof of the antecedent can be extended to a proof of the consequent.)

The translation function (12) can be compactified as follows: τ(A) results from boxing all subformulas of A that are either atoms, negations or implications. For example, τ(¬p) = □ ¬□p = □⋄¬p, τ(p ∨ q) = □p ∨ □q, τ(p → q) = □ (□p → □q). The following translation theorem has been proved by McKinsey and Tarski (1948):

• (13) Theorem (L_int into S4): Γ |==_int A iff τ(Γ) |==_S4 τ(A).

For example, |=/=_S4 τ(p ∨ ¬p) holds, since τ(p ∨ ¬p) = □p ∨ □¬□p and |=/=_S4 □p ∨ □¬□p.

3.3 Translating paraconsistent logic

The strategy of translating the paraconsistent logic LP into classical logic L₂ is the same as for L₃ as outlined in Sect. 3.1: we extend ${\mathcal{L}}_{2}$ by the three intensional operators T^LP (true only), B^LP (both true and false) and F^LP (false only) and represent their truth-tables as axioms of the modal theory Ax_LP in the extended language ${\mathcal{L}}_{{_{{{2}.{\text{para}}}} }}$. Let "D(A)" stand for "A has a designated truth value", being an abbreviation for "T^LP(A) ∨ B^LP(A)". Then the translation theorem is analogous to theorem (10), but with T³(A) and T³(Γ) replaced by D(A) and D(Γ), respectively (where D(Γ): = {D(B): B ∈ Γ}):

• (14) Theorem (LP into L₂): Γ |==_LP A iff Ax_LP ∪ D(Γ) |==_L2 D(A).

Based on this translation we can show, for example, that D(p ∧ ¬p) |=/= D(q), and likewise that D(p ∨ q), D(¬p) |=/= D(q) and D(p → q), D(p) |=/= D(q) (etc.), i.e., the translations of LP-invalid inferences come out as invalid, too.

There is nevertheless an important difference between the translation of L₃ and that of LP: While the trivalent truth operators T³, U³ and F³, whose values are always bivalent, are explicitly definable in L₃, the corresponding truth operators T^LP, B^LP and F^LP are undefinable in LP—ultimately because of the tiny difference that b → b = b (instead of b → b = t). This makes it impossible to define "Bp" via "(p ∨ ¬p) → (p ∧ ¬p)". Therefore, the translation of LP into L₂ yields a proper expressive extension of LP: in L₂ ∪ Ax_LP we can express and prove inferences that are inexpressible in LP, as for example:

• (15) T^LP(p ∧ ¬p) |==₂ T^LPq; T^LP(p ∨ q), T^LP(¬p) |==₂ T^LPq; T^LP(p → q), T^LPp |==₂ T^LPq,

which are the T^LP-modalized versions of EFQ, DS and MP, that are valid in LP, but inexpressible in LP.

3.4 Translating quantum logic

A well-known method of translating QL (quantum logic) into extended classical logic translates orthologic OL into the modal logic B. OL is a slight weakening of QL that results from classical logic by removing the expansion version of distribution (D_e). Algebraically OL is characterized by the class of ortholattices; these are Boolean lattices without distributivity (Dalla Chiara & Giuntini, 2002, p. 137). QL strengthens OL by a weakened distribution rule that is satisfied by the lattice of quantum propositions, namely 'orthomodularity' (O): p ∧ (¬_qp ∨ _q (p ∧ q)) |==_QL q (ibid., p. 142).

The modal logic B, in which OL is translated, is semantically characterized by reflexive and symmetric Kripke frames and satisfies the axioms (B): A → □⋄A (corresponding to the symmetry of R) as well as (T), (K) and the rule (N) (see Sect. 3.2). Dishkant (1972) proved that OL is complete for the class of generalized B-frames <W, R, Π> whose worlds are physical states, whose accessibility relation is interpreted as the negation of orthogonality (Rαβ iff α·β ≠ 0), and whose algebra of admissible propositions Π ⊆ Pow(W) contains W, is closed under the operation of orthocomplement X^oc (the semantic counterpart of quantum negation), and satisfies the following condition:

• (*) (∀β ∈ R_{α} ∃γ ∈ R_{β}(γ ∈ X)) → α ∈ X, for all X ∈ Π,

where R_{α} is the set of worlds R-accessible by α (Dalla Chiara & Giuntini, 2002, pp. 138–140). Condition (*) guarantees closure of worlds under linear combinations and implies X = (X^oc)^oc. Generalized Kripke frames of this kind (with val(¬_qA) =||A||^oc and val(A ∧ B) = val(A) ∩ val(B)) are called orthoframes. Following from (*) one can prove that a statement A is true at a world α in an orthoframe F if and only if □⋄A is true at α in F (ibid. 140, theorem 11), where the only-if direction is the non-trivial part (the if-direction is an instance of axiom B). This fact leads directly to the method of translating OL-statements into the logic B with the classical (i.e. unrestricted) algebra of propositions (Π = Pow(W)) as follows. The informal interpretation of the translating condition is stated in brackets; it relies on the (provable but not immediately obvious) fact that "□⋄A" holds in an actual state α iff all physical states that are accessible by measuring α verify A; this is the modal-logical rephrasing of the informal interpretation "measurement will verify A with certainty" given in Sect. 2.4.

• (16) Translation (τ) from OL into B:

  For all p ∈ ${\mathcal{P}}$: τ(p) = □⋄p (All measurement-accessible states verify p.)

  τ(¬_qA) = □ ¬τ(A)  (No measurement-accessible state verifies A's translation.)

  τ(A ∧ B) =  τ(A) ∧ τ(B)  (All measurement-accessible states verify A's translation and verify B's translation.)

  τ(A ∨_q B)  = _def  τ(¬_q(¬_qA ∧ ¬_qB)) = □ ¬ (□¬ τ(A) ∧ □¬ τ(B)) ≡ □ (⋄τ(A) ∨ ⋄τ(B)).  (All measurement-accessible states verify A's translation or verify B's translation.)

Based on this translation one can prove (Goldblatt, 1974; Dalla Chiara & Giuntini, 2002, theorem 53):

• (17) Theorem (OL into B): Γ |==_OL A iff τ( Γ) |==_B τ(A).

The translation (17) can be extended to the system QL by adding the modal translation of the rule O (see above); however, the rule O cannot be characterized by an elementary frame-condition (ibid., 162).

A second translation method was developed by theoretical physicists and logicians (Baltag & Smets, 2011) and consists in translating QL into dynamic modal logic. Because of space limitations we cannot present this powerful method in this paper; for a discussion within the proposed translation approach see Schurz (2021b, (12)).

4 Epistemological conclusions and possible objections

4.1 Representational optimality and commensurable pluralism

In the previous section it was shown that major kinds of non-classical logics are translatable into extended classical logic. We conjecture that all non-classical logics can be translated into a suitably extended classical logic. Our reason for this conjecture is that all non-classical logics known to us can be semantically described in a classical metalogic.

If our arguments are correct, they give us an optimality justification of classical logic in regard to the epistemic goal of representational power. An optimality justification does not attempt to prove that a given epistemic method is correct or reliable. It pursues the more modest epistemic goal of demonstrating that a given method is epistemically optimal among all competing methods that are cognitively accessible. The method of optimality justifications has been developed as an approach to the problem of induction (Schurz, 2019). In this section it is applied to the problem of justifying classical logic. The optimality justification we propose is as follows: by using classical logic we can only gain, but not lose, because if another logic has advantages for certain purposes, we can embed it into classical logic.

What is primarily achieved by our result is the removal of the first threat mentioned in Sect. 2: the threat of epistemic incommensurability. We rather are in the situation of a commensurable logical pluralism, in which classical logic plays the 'privileged' role of a global unifying framework. Our result has significant consequences for recent controversies on different versions of logical pluralism that can be mentioned here only briefly. For example, it makes it possible to overcome the restrictions of contextualist pluralism, insofar as non-classical and classical assertions, that according to contextualism can only be asserted in different contexts (cf. Caret, 2017), can now be simultaneously expressed in a unified 'context'. For example, in L_2.Luk we can express that a proposition p is undetermined from a three-valued perspective but false from a two-valued perspective: U³p ∧ ¬p. Assertions of this sort are of importance for rational deliberations about which 'context' one should assume.

4.2 The possibility of inverse translation—optimality without dominance?

In this section we ask: is classical logic the only logic that is representationally optimal? Or can a non-classical logic also be representationally optimal in the sense that an inverse translation of classical logic into it is possible? The answer to this question is: predominantly no, but in some cases yes.

Before we explain this answer, let us clarify the possible reach of this objection: if it were true, it would not refute the optimality thesis, but merely the dominance thesis for classical logic. The two notions come from game theory (cf. Schurz, 2019, Sect. 5.7). A method (here a logic) is optimal w.r.t the class of cognitively accessible methods iff it has maximal value in this class in regard to a given goal, here representation power. The optimality of a logic L does not exclude the possibility of other logics that have the same maximal value; thus there may be many logics which are equally optimal. This situation would only be excluded if a logic L is dominant, which means that L has a higher value than all other logics.

However, the optimality-dominance distinction does not fully defeat the intertranslatability objection. The opponent may continue: if some non-classical logics are also optimal, what has been achieved by the optimality justification of classical logic? The answer was given in Sect. 4.1: the first threat, epistemic incommensurability, is defeated by optimality, but not the second threat, subjective relativism. If there are many equally representation-optimal logics L₁,…,L_n, and there are no further ceteris paribus preferences between them, then the rational choice among them is still undetermined and a matter of taste. Below we will argue that the situation is nevertheless not symmetric and classical logic has important ceteris paribus advantages as a unifying metalogic. Before we turn to this point we consider inverse translations in more detail.

Consider the translation τ_3→2 of Lukasiewicz' logic L₃ into classical L₂ described in Sect. 3.1. An inverse translation τ_2→3 is possible in complete analogy to τ_3→2 by extending L₃ by the two truth-value operators T² and F² of two-valued logics. In L₂ the two operators are explicitly definable as T²A ↔ A and F²A ↔ ¬A. In L₃, T² and F² figure as intensional operators axiomatized by the obvious set of equivalence axioms Ax_class in the extended language ${\mathcal{L}}_{{{3}.{\text{class}}}}$ (for negation: T²(¬A) ↔ F²(A); F²(¬A) ↔ T²(A); for conjunction: T²(A ∧ B) ↔ T²(A) ∧ T²(B); F²(A ∧ B) ↔ F²(A) ∨ F²(B); etc.), together with the bivalence axiom T²(A) $\dot{\vee}$ F²(A). The translation of ${\mathcal{L}}_{2}$-formulas into ${\mathcal{L}}_{3}$-formulas is again based on the truth view of assertion: τ_2→3(A) = T²(A), for every A ∈ ${\mathcal{L}}_{2}$. Examples (with τ_2→3 = τ): τ(p) = T²p, τ(¬p) = F²p, τ(p ∨ ¬p) = T²(p ∨ ¬p) ≡ T²p ∨ F²p, τ(p ∧ ¬p) = T²(p ∧ ¬p) ≡ T²p ∧ F²p, τ(p → q) = T²(p → q) ≡ F²p ∨ T²q, etc. Based on this translation, the following theorem is proved in Schurz (2021b, Sect. 6.1), in complete analogy to theorem (10) of Sect. 3.1:

• (18) Theorem (L₂ into L₃):

  (1.) Every bivalent valuation function val₂ over ${\mathcal{L}}_{2}$ corresponds exactly to a trivalent valuation function val₃ over ${\mathcal{L}}_{{{3}.{\text{class,}}\tau }}$ satisfying the axioms Ax_class such that for every ${\mathcal{L}}_{2}$-formula A: val₂(A) = o² iff val₃(O²(A)) = t, where o² = t²/f² iff O² = T²/F².

  (2.) Γ |==_L2 A iff Ax_class ∪ T²(Γ) |==_L3 T²(A).

For sake of semantic coherence between L₂ and L₃ we require the two bridge axioms in L₃: For all p ∈ ${\mathcal{P}}$, (i) T³p → T²p and (ii) F³p → F²p. Note that we cannot express the bridge axioms as (i) p → T²p and (ii) ¬p → F²p, because in L₃, p and T³p are not equivalent, and neither are ¬p and F³p.

A similar translation of L₂ is possible for all n-valued logics that have "truth" as a designated value and within which the operations of n-valued truth resp. falsity are definable. For many other non-classical logics, however, it is impossible to embed classical logic via translation. There are two possible reasons for this. First, the translation is technically impossible, because the non-classical logic is too weak. Second, the translation would be technically possible, but is philosophically inadequate. The first possibility applies to paraconsistent and quantum logic and the second possibility applies to intuitionistic logic.

For the system LP of paraconsistent logic the translation method fails, because LP's designated values are T³ and B³, and it is impossible to define truth-only (T³) in LP (as explained in Sect. 3.3). Therefore the axiom T²(A) $\dot{\vee}$ F²(A) (together with T²(¬A) ↔ F²(A) and F²(¬A) ↔ T²(A)) cannot enforce in LP that T²(A) and F²(A) are bivalent (either true-only or false-only); the designatedness of T²(A)$\dot{\vee}$ F²(A) is compatible with T²(A) and F²(A) having the value b. Thus the representational power of LP is strictly weaker than that of L₂ or L₃.⁶

A translation of classical logic into quantum logic QL appears also to be impossible. Since the implicit semantics of QL is bivalent, the introduction of an intensional truth operator T² would be useless, because it would satisfy the correspondence axiom T²(A) ↔ A. What would be needed is a translation of classical negation and disjunction, τ(¬A) and τ(A ∨ B), into QL-formulas that behave like the classical connectives, but such formulas do not exist.

In intuitionistic logic, the translation of L₂ into L_int could be technically carried out in the same way as for L₃, by extending the intuitionistic language ${\mathcal{L}}_{{{\text{int}}}}$ by the bivalent operators T², F² and adding the axiom set Ax_class. Thus the translation is technically possible; however, it would be philosophically inadequate. The translation would allow one to derive the bivalence axiom T²(A) ∨ ¬T²(A) for L₂-translations, but L_int's assertions are based on the proof view of assertion. According to this view the validity of T²(A) ∨ ¬T²(A) in L_int means that one can prove this disjunction and thus can prove either T²(A) or ¬T²(A), for every formula A; but this is against the spirit of intuitionistic logic which admits propositions whose truth value is not decidable by proof.

4.3 Global ceteris paribus advantages of classical logic

In the previous section we have seen that L₂ is not the only representationally optimal logic; some alternative non-classical logics are representationally optimal, too. Thus, the justification strategy based on translatability reduces the large diversity of non-classical logics to a small class of logics that are representationally optimal, but it does not yield a unique preference for classical logic. Does this mean that we cannot give a preference (or dominance) argument for classical logic—even not for the role of a unifying metalogic? The answer to this question is directly relevant to the controversy about local versus global logical pluralism (Hjortland, 2013, p. 356f). If only classical logic can figure as a unifying metalogic, then logical pluralism is merely local, insofar non-classical logics may have simplicity advantages in particular domains (see Sect. 4.4). However, if a non-classical logics could fit the role of a unifying metalogic equally well as classical logic, this would speak in favor of a global pluralism.

We argue that in spite of the intertranslatability of L₂ with some many-valued logics, the situation is not symmetric. Classical logic has two further global ceteris paribus advantages as a unifying metalogic that go beyond its representational optimality. These advantages privilege classical logic even over those non-classical logics that are representationally optimal in the sense of the translation argument:

• 1. Determinateness in the metalogic: Theoreticians as well as applicants of logics are interested in logical frameworks whose syntactic and semantic properties are determined. We do not want a notion of proof for which the question of whether a conclusion follows from a premise set is irreducibly indeterminate. Nor are we interested in a logical system whose consistency is indeterminate (etc.). This speaks in favor of using not a trivalent, but a classical bivalent logic as metalogic. Should there really arise a situation where we encounter an irreducible indeterminateness, we can express this by using intensional operators.

• 2. Naturalness and induction from practice: It is common practice to discuss the pros and cons of competing logics within a classical metalogic. Likewise it is common practice in mathematical logic to use classical metalogic for the semantics of a non-classical logic. These facts of our practice don't 'prove' anything, and there are exceptions, e.g., constructivist mathematicians using an intuitionistic metalogic. However, these facts seem to confirm the thesis that a bivalent classical metalogic is the most natural choice of a framework for the comparison and evaluation of competing systems of logic. Admittedly it is true that the classical notion of inference has problems with relevance; but as explained in Sect. 3.2, these problems can also be handled by relevance filters within classical logic.

4.4 Local advantages of classical and non-classical logics

A final important ceteris paribus criterion for the choice of logics is its simplicity. In this section we ask: what follows from the simplicity criterion for the choice of a logic in a given context of application?

Assume we are in a context of application in which our descriptions require the logical operations of a certain non-classical logic L_n. Then the question is: what is simpler—using L_n directly or using the translation of L_n into the corresponding extension L_2.n of classical logic? So far this question is largely left undecided by our considerations.

The answer to this question depends on the context of application, which consists of (i) a particular domain and (ii) of a particular purpose (cf. Bueno, 2010, p. 115). As a first example, consider the domain of quantum-physical states with the purpose of describing their abstract structure. The logical representation of linear combinations and orthocomplements of quantum-physical states is simpler in QL than in QL's translation into classical logic (Ashcroft, 2010, p. 185). On the other hand, if we want to express that a quantum system is in a pure versus a superposed state, we need in addition the resources of classical logic (recall Sect. 2.4), which speaks in favor of using one of the two possible translations of QL into the extended classical logic. Since QL is bivalent in its semantics, there are no problems in the ontological interpretation of QL-negation and QL-disjunction within the extended classical framework.

As a second example, consider Lukasiewicz' three-valued logic. Assume we have good reasons for thinking that certain propositions describing our domain are undetermined. If there are only a few propositions of this sort and most propositions are adequately described in L₂, then using the extended logic L_2.Luk is clearly preferable to a complicated 'context-switching' between L₃ and L₂. On the other hand, in a domain where more-or-less all propositions are three-valued—if such a domain exists—, the employment of L₃ throughout would be simpler than using L₃'s translation in L_2.Luk.

In the case of a three-valued (or many-valued) logic represented in the extended classical logic L_2.Luk, the question of its ontological interpretation is not so straightforward as in quantum logic. For in L_2.Luk, sentences p that are regarded as undetermined in L₃ are nevertheless bivalently true or false, i.e., U³p ∧ p or U³p ∧ ¬p will hold. The question is how we should interpret the bivalent truth values of undetermined sentences in L_2.Luk. In other words, even if the epistemological question is settled in favor of using an extended classical logic, the metaphysical question of the ontological interpretation of indeterminacy is still open. There are two possibilities. (i) We may assume that the bivalent truth value of an undetermined proposition p is epistemically inaccessible in an insuperable way, but nevertheless p is objectively determined, i.e., the bivalent truth values are real in the correspondence-theoretic sense. (ii) Or we believe that p is objectively undetermined, in which case we must consider the bivalent truth values as an epistemic idealization, comparable to imaginary numbers that do not correspond to physical properties, but are nevertheless useful for describing physical systems.

Moreover, we have to ask: what kind of truth is asserted when we assert p in the system L_2.Luk: do we assert that p is bivalently true, or stronger, that it is trivalently true? According to the 'lexical' meaning of an assertion of p in L_2.Luk, only p's bivalent truth is asserted. However, it is reasonable to assume that the speaker also believes in p's trivalent truth, as long as not stated otherwise. Therefore we suggest to employ in L_2.Luk the following default principle: as long as it is not explicitly stated that an asserted proposition p is objectively undetermined, we assume by default that p is trivalently true. More formally, if Γ is the set of assertions made in L_2.Luk, then for a given A ∈ Γ such that Γ |=/= U³(A), T³(A) is added to Γ. This proposal leads immediately to the problems well-known from non-monotonic and default logic: it may happen that the addition of T³(A) to Γ for all A ∈ Γ with Γ |=/= U³(A) leads to inconsistency. One example of such a set is Γ = {p, T³p → U³q, q}, to which we can add T³p or T³q but not both (since T³p implies U³q, which entails ¬T₃q by Ax_Luk). Different ways of handling this difficulty have been proposed in the literature (Strasser & Antonelli, 2019) that cannot be discussed here; an interesting possibility would be the application of adaptive logic (Batens, 2007).

4.5 Final conclusions

In this paper we have argued that in respect to the question of justification, systems of logic are exceptional, but not a priori necessary. Logics are exceptional, because they cannot be demonstrated as valid or confirmed by observation without entering a circle, and their motivation based on intuition is unreliable. On the other side, systems of logics do not express a priori necessities of thinking, because alternative non-classical logics have been developed. By means of a brief tour through the controversies about four major kinds of non-classical logic in Sect. 2 we have seen that there is no particular domain or reason that would enforce the use of a non-classical logic; the particular reasons given for a non-classical logic can also be handled within classical logic. This result was substantiated in Sect. 3, where it was shown that all four kinds of non-classical logics can be translated into extended systems of classical logics in a meaning-preserving way.

Based on this fact we have argued in Sect. 4 that classical logic is representationally optimal. However, classical logic is not the only logic with this desirable property; not many but a few non-classical logics are likewise representationally optimal. In the final section we argued that nevertheless the situation is not symmetric: classical logic has important ceteris paribus advantages as a unifying metalogic. On the other hand, non-classical logics can have local simplicity advantages.