| Citation: | Wang YQ, Zhang JH, Zheng YC, Xu YR, Xu JQ et al. Brillouin scattering spectrum for liquid detection and applications in oceanography. Opto-Electron Adv 6, 220016 (2023). doi: 10.29026/oea.2023.220016 |
Brillouin scattering spectrum for liquid detection and applications in oceanography
-
Abstract
The Brillouin scattering spectrum has been used to investigate the properties of a liquid medium. Here, we propose an improved method based on the double-edge technique to obtain the Brillouin spectrum of a liquid. We calculated the transmission ratios and deduced the Brillouin shift and linewidth to construct the Brillouin spectrum by extracting the Brillouin edge signal through filtered double-edge data. We built a detection system to test the performance of this method and measured the Brillouin spectrum for distilled water at different temperatures and compared it with the theoretical prediction. The observed difference between the experimental and theoretical values for Brillouin shift and linewidth is less than 4.3 MHz and 3.2 MHz, respectively. Moreover, based on the double-edge technique, the accuracy of the extracted temperatures and salinity is approximately 0.1 °C and 0.5%, respectively, indicating significant potential for application in water detection and oceanography.-
Keywords:
- Brillouin scattering spectrum /
- double-edge technique /
- temperature /
- salinity /
- oceanography
-
Introduction
The concept of light scattering was better understood after explaining why the sky is blue by Lord Rayleigh in 18711. Einstein2 further related scattered light to refractive index fluctuations and noticed that the determining factor for these fluctuations is density fluctuations. These observations formed the main pioneering study of Rayleigh scattering3-4. Later, light scattering by adiabatic fluctuations (inelastic scattering, the fine structure of the Rayleigh line) of the density fluctuations was first investigated by Mandel’shtam in 19185 and proposed independently by Brillouin in 19226. Since then, this inelastic scattering, named Brillouin scattering, has been well studied in gases7-12, liquids13-16, and solids17-22.
Brillouin scattering refers to the acoustic modes that manifest as Brillouin peaks away from the central Rayleigh peak in the spectrum. As these dynamics depend on the scattering medium’s properties, the optical resolution of the Brillouin spectrum can be used to analyze the elastic properties, such as the velocity and attenuation of sound. The physical properties of the medium can be deduced based on the Brillouin spectrum. For Brillouin scattering in liquids, the Brillouin spectrum generally adopts a Lorentzian functional form3, 23. This clear and simple analytical feature of the spectrum provides unique advantages for further applications. For instance, in water, by detecting whether the Brillouin peaks appear, one can judge the existence of the submerged object24. In addition, the Brillouin shift and Brillouin linewidth can be extracted from the Brillouin spectrum and used to calculate related physical quantities, such as temperature25-27, sound velocity28, 29, and bulk viscosity30, 31. Currently, the measurement of the Brillouin spectrum has become an important method for detecting the inner physical properties of matter.
Experimentally, there are two typical techniques for obtaining the complete Brillouin spectrum32. The first technique involves using the Fabry–Perot etalon (FPE) and intensifier charge-couple device (ICCD)33, 34. Through FPE, a 2D interference fringe pattern of Rayleigh–Brillouin (RB) scattering will be recorded on the ICCD. The pattern contains the entire spectrum information to enable the extraction of the Brillouin scattering characteristics. However, this technique is limited by the response threshold of ICCD and the extra measurement error caused by the ICCD pixel size. The other technique involves using Fabry Perot interferometer (FPI) and photomultiplier tube (PMT)29, 35. In this method, the entire spectrum was obtained by scanning the FPI and the accuracy of the water temperature is 3 °C. Unfortunately, this method is not suitable for real time application because the scanning process is time-consuming. For practical applications, these two techniques have their respective deficiencies. Thus, it is highly desirable to explore new methods to improve Brillouin spectrum measurement.
Generally, the Brillouin spectrum of a liquid indicates a Lorentzian line shape. The spectrum can be determined if the Brillouin peak position (Brillouin shift) and the full width at half maximum (Brillouin linewidth) are known. Recently, the edge technique was proposed to measure the Brillouin shift; it was used for real-time applications in remote sensing applications in the ocean36. Its principle is to measure a small frequency shift based on measuring a large intensity variation, and the Brillouin shift can be obtained from the normalized variation of the intensity. The accuracy of the water temperature measured by the Brillouin shift in this technique can reach 0.5 °C(averaging 1000 laser shots)37. However, as it obtains only the signal intensity rather than the spectrum, considerable information will be lost. In reality, the normalized intensity is also affected by the Brillouin width. In the experiments, the Brillouin shift and Brillouin linewidth can be obtained simultaneously if two normalized intensities are measured.
Based on this feature, we propose a new method based on a double-edge technique. When the liquid environment varies, the Brillouin spectrum is different, and the energy intensities after the two filters also change. The Brillouin scattering spectrum can be reconstructed after building relationships between energy intensities and Brillouin spectrum characteristics. This improved method can measure the whole Brillouin scattering spectrum and inherit the advantages of the edge technique, indicating its potential application in liquid detection. The remainder of this paper is organized as follows. In Section Theory and experiment, the measurement theory and experimental setup are presented. The results are presented and discussed in Section Results and discussion to analyze the performance of the proposed method. Finally, the conclusion is presented in the last section.
Theory and experiment
Theory
Light propagating in a transparent liquid is scattered by the density fluctuations of the liquid medium. The density fluctuations can be expressed by entropy fluctuations at constant pressure and pressure (acoustic) fluctuations at constant entropy; the former corresponds to Rayleigh scattering, and the latter leads to Brillouin scattering. In the view of quantum physics, Brillouin scattering is considered as the process of incident photon releasing/absorbing a phonon, producing two kinds of scattered photons of different frequencies, as shown in Fig. 1(a). The scattering that releases phonons and makes the frequency smaller than the incident light frequency is the Stokes scattering, and the contrary phenomenon is the anti-Stokes scattering. The Stokes and anti-Stokes peaks are symmetrically distributed on both sides of the central Rayleigh peak. When the medium environment changes, the Brillouin spectrum also changes. Fig. 1(b) displays the Brillouin Stokes spectrum of water, which varies with temperature.
 Figure 1. (a) Vector diagram of Brillouin scattering in view of quantum physics with the process of incident photon releasing and absorbing a phonon. (b) Brillouin spectra of water varies as the temperature changes. (c) Principle of the Brillouin spectrum measurement using double edge technique. Two edge filters are set at the steep edge of the Brillouin Stokes spectrum BS(vB, ΓB ), where vB is the Brillouin shift ΓB and is the Brillouin linewidth. For BS, the energies after these two filters are I1(vB, ΓB ) and I2(vB, ΓB). vB and ΓB can be deduced from I1 and I2, and Brillouin spectrum BS can be reconstructed. When the Brillouin spectrum changes to BS′, new energies
Figure 1. (a) Vector diagram of Brillouin scattering in view of quantum physics with the process of incident photon releasing and absorbing a phonon. (b) Brillouin spectra of water varies as the temperature changes. (c) Principle of the Brillouin spectrum measurement using double edge technique. Two edge filters are set at the steep edge of the Brillouin Stokes spectrum BS(vB, ΓB ), where vB is the Brillouin shift ΓB and is the Brillouin linewidth. For BS, the energies after these two filters are I1(vB, ΓB ) and I2(vB, ΓB). vB and ΓB can be deduced from I1 and I2, and Brillouin spectrum BS can be reconstructed. When the Brillouin spectrum changes to BS′, new energiesI′1 andI′2 will be acquired and the corresponding Brillouin shift and linewidth can be deduced and used for BS′ reconstruction.In the case of Brillouin scattering in liquid, the medium can be treated as a continuum, broadening effects are homogeneous, and both Stokes and anti-Stokes peaks adopt a Lorentzian functional form as:.
IB(vB,ΓB)=1π{ΓB4(v−vB)2+Γ2B+ΓB4(v+vB)2+Γ2B}, (1) where vB is the Brillouin shift and ΓB is the Brillouin linewidth. If vB and ΓB are known, the Brillouin spectrum can be easily restructured.
Recently, edge techniques have been widely used to detect the Brillouin echo signal since it was first proposed in ocean applications by Fry et al.36; in their study, the Brillouin spectrum is locked at a steep transmittance curve. The slightest variation in the Brillouin shift causes a large change in the transmitted energy. Therefore, the Brillouin shift can be measured by detecting this energy. In real applications, the related energy change is used to reduce the influence of the energy intensity instability. More specifically, the central Rayleigh and Mie scattering is first filtered by an absorption filter, and then the filtered scattering light is split into two parts: One is directly received by the detector as the reference signal, Ig. The other goes through an iodine cell used as the edge filter and recorded by another detector as I1. The related energy change S= I1/Ig was used for the Brillouin shift measurement.
In fact, the relative energy change S is not only affected by the Brillouin shift, but also depends on the Brillouin linewidth. The key point is that the Brillouin shift and linewidth can be measured using two different related energies. Hence, the edge technique can be improved by using double edges simultaneously, as shown in Fig. 1(c).
For the double-edge method, the back RB scattering signal first passes through an absorption filter to eliminate the Rayleigh scattered light. Then, one part of the remaining Brillouin light is used as the reference energy Ig and detected by a PMT. The other part yields into a double-edge filter designed to allow the energy of the steep edge on the two sides of the Brillouin peak to pass. Light after the double-edge filter is detected by two other PMTs, I1 and I2. Here we have:
Ig=∫ + ∞−∞IB(v,vB)dv, (2) I1=∫ + ∞−∞T1(v−v1,Γ1)IB(vB,ΓB)dv, (3) I2=∫ + ∞−∞T2(v−v2,Γ2)IB(vB,ΓB)dv, (4) Ti(i=1,2) is the instrument function of the ith edge filter, expressed by the Airy function:
Ti=[1+(2FSRiπΓi)2 sin2(πFSRiv)]−1, (5) FSRi is the free-spectrum range of the ith filter. Γi is the linewidth of the ith filter.
Then the relative energy S1 and S2 are written as:
S1=I1Ig,S2=I2Ig. (6) The dependency of the Brillouin shift and Brillouin linewidth on S1 and S2 can be obtained by establishing a retrieval model38:
{vB(S1,S2)=r1+r2ln(S1)+r3ln(S2)+r4ln(S1)2+r5ln(S2)2+r6ln(S1)ln(S2)+r7ln(S1)3+r8ln(S2)3+r9ln(S1)ln(S2)2+r10ln(S1)2ln(S2)ΓB(S1,S2)=t1+t2ln(S1)+t3S2+t4ln(S1)2+t5(S2)2+t6ln(S1)S2+t7ln((S1)3)+t8(S2)3+t9ln(S1)(S2)2+t10ln(S1)2S2, (7) in which coefficients ri and ti can be found in ref.38. Therefore, when S1 and S2 are detected, the Brillouin shift and linewidth can be calculated, and the Brillouin spectrum can be reconstructed. Moreover, the environmental information of the liquid, such as the temperature or salinity of water, can be extracted based on the Brillouin spectrum26, as Eq. (8) shown:
{T(vB,ΓB)=m1+m2vB+m3ΓB+m4v2B+m5Γ2B+m6vBΓB+m7v3B+m8Γ3B+m9vBΓ2B+m10v2BΓBS(vB,ΓB)=k1+k2vB+k3v2B+k4v3B+k5v4B+k6v5B+k7lnΓB+k8lnΓ2B+k9lnΓ3B+k10lnΓ4B+k11lnΓ5B , (8) where coefficients mi and ki are displayed in ref.26. The simulation of the retravel model shows that this double-edge technique can be used to measure the temperature and salinity of the water in the temperature range of 0–30 °C and salinity range of 0–35%.
Experimental apparatus
A setup built for the Brillouin spectrum measurement was used to evaluate the performance of the double-edge method. As shown in Fig. 2, the experimental apparatus comprises the following: pulse laser, telescope for receiving scattered light, water tank for producing scattered light, iodine tube to filter the Rayleigh and Mie scattering light, double-edge filter that lets the two sides of one Brillouin peak get through, and three PMTs to detect the corresponding intensity of Brillouin light. The apparatus and units are further described in the following subsections.
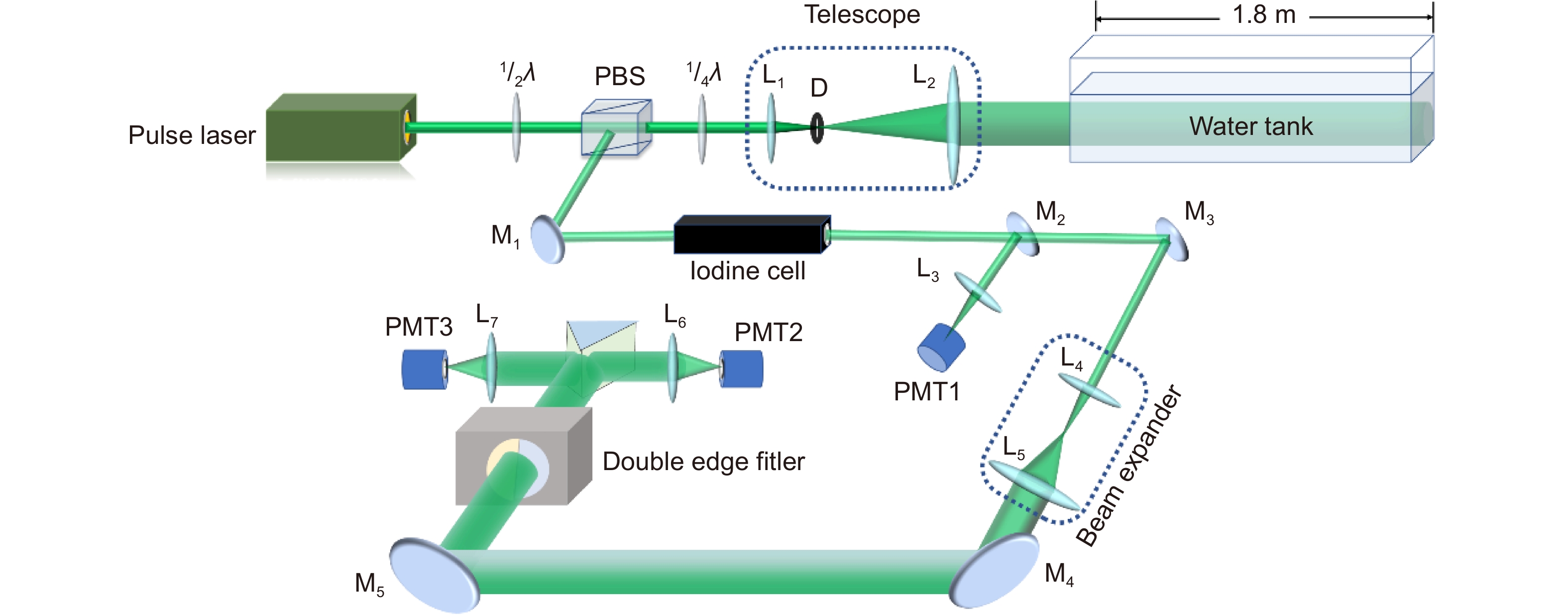 Figure 2. Sketch of experimental apparatus. Pulse light of wavelength 532.293 nm with pulse width of approximately 7.5 ns, repetition rate of 100 Hz, and pulse energy of 20 mJ goes through a half waveplate, a polarization beam splitter (PBS), and a quarter-wave plate successively. Then the light is spread by a telescope combined by two convex lenses, L1 (f=0.5 m) and L2 (f = 0.1 m), and yields into a water tank of 1.8 m length and 0.5 m width to produce scattering light. The 180º back scattering light is received by the telescope and reflected by the PBS to an iodine tube which can absorb the Rayleigh part. The scattering light after the iodine tube is split into two by M2. One small fraction beam is detected by the first photomultiplier tube (PMT1) as reference energy. The other part enters to a double-edge filter which is made by two Fabry-Perot interferometers and the light beams after these two interferometers are accepted by PMT2 and PMT3 separately. D is diaphragm, Mi and Li (i=1, 2..) are mirrors and lens, respectively.
Figure 2. Sketch of experimental apparatus. Pulse light of wavelength 532.293 nm with pulse width of approximately 7.5 ns, repetition rate of 100 Hz, and pulse energy of 20 mJ goes through a half waveplate, a polarization beam splitter (PBS), and a quarter-wave plate successively. Then the light is spread by a telescope combined by two convex lenses, L1 (f=0.5 m) and L2 (f = 0.1 m), and yields into a water tank of 1.8 m length and 0.5 m width to produce scattering light. The 180º back scattering light is received by the telescope and reflected by the PBS to an iodine tube which can absorb the Rayleigh part. The scattering light after the iodine tube is split into two by M2. One small fraction beam is detected by the first photomultiplier tube (PMT1) as reference energy. The other part enters to a double-edge filter which is made by two Fabry-Perot interferometers and the light beams after these two interferometers are accepted by PMT2 and PMT3 separately. D is diaphragm, Mi and Li (i=1, 2..) are mirrors and lens, respectively.Light source
The pulsed laser in this setup uses seed injection technology to achieve a single longitudinal mode and narrow linewidth output. The laser frequency is locked to the edge of the absorption line of the iodine pool through iodine molecular frequency stabilization technology, and then the laser output frequency is shifted to the middle position of the absorption peak. This laser outputs pulsed light with a wavelength of 532 nm and an uncertainty of 0.0005 nm. The repetition frequency was 100 Hz with a pulse width of 7.5 ns and energy of ≥20 mJ for each pulse.
Characteristic analysis of absorption filter
The absorption filter is used to eliminate all elastically scattered light, with the central frequency same as the laser frequency, and only leaves Brillouin components. For this, an iodine cell was chosen as the absorption filter as the iodine generated absorption around the light at 532 nm. After simulation of the iodine, a proper absorption line was chosen with a laser wavelength of 532.239 nm. Considering the maximum Rayleigh filtering and Brillouin side transmission, the temperature of the iodine cell was controlled at 40±0.01 °C.
Double-edge filter
The double-edge filter consists of two plane mirrors. Considering the Brillouin shift and linewidth of the water in the temperature range of 0–30 °C and salinity range of 0–35% are around 7.4 GHz and 0.5 GHz respectively with the laser wavelength of 532 nm. The inner surface is coated with a reflective film and half of the edge filter is plated with a step film of about 40 nm, making the edge a double-channel etalon. The slight difference between the double-channel lengths causes the peak transmission frequency of the two channels to have a fixed difference. The two etalon channels are integrated on the same component and share the same set of temperature control systems, which helps to improve the thermal and mechanical stability of the actual system. After testing, the FSR of the two channels is 24.82 GHz. The central frequency and linewidth of one half etalon are –9.51 GHz and 0.77 GHz and for the other half etalon, –5.44 GHz and 0.73 GHz. The minus sign indicates that the double-edge etalon is working in the location of the Brillouin Stokes location.
Data acquisition
As the energy after the double edge is weak, the PMT (HAMAMATSU-H11526-01-NF, Hamamatsu) was used to detect the signal. The PMT is connected by a transimpedance amplifier (C1184, Hamamatsu), and the voltage signal after the amplifier is recorded by a high-speed acquisition card (ADQ12DC, Teledyne SP Devices), which provides a 12-bit resolution and a sampling rate of 1 GS/s per channel.
Results and discussion
In this section, we present the experimental data on Brillouin scattering in water and discuss Brillouin characteristics and spectrum reconstruction. We also evaluate the accuracy of the retrieved temperature and salinity of water under different conditions based on this double-edge method.
The experiments were performed using distilled water. The pulsed light enters the water tank, producing a 180° back-scattering RB scattering signal. After passing through the iodine cell, Brillouin light was detected by three PMTs. Figure 3(a) shows the voltage for 200 successive shots recorded from PMT1 and their average for water at room temperature. The upper spatial axis is computed from the lower time axis, where the time of the pulse peak out of the telescope corresponds to 0 m. As shown in Fig. 3, the averaged curve becomes smooth, although shot fluctuations exist in the single shots. The oscillation at the end of the signal originates from the power supply noise. Fig. 3(c) and 3(e) show the corresponding edge signals recorded by PMT2 and PMT3, respectively. As there is a distance between PMT1 and PMT2/PMT3, the peak signals from PMT1 and PMT2/PMT3 have a time difference of 6.2 ns.
 Figure 3. Spatially resolved Brillouin backscatter intensity from the water tank at room temperature recorded (a) by PMT1 (c) by PMT2 (e) by PMT3 with 200 successive shots (color lines) and their average (white dots) and the corresponding background noise measured by (b) by PMT1 (d) by PMT2 (f) by PMT3.
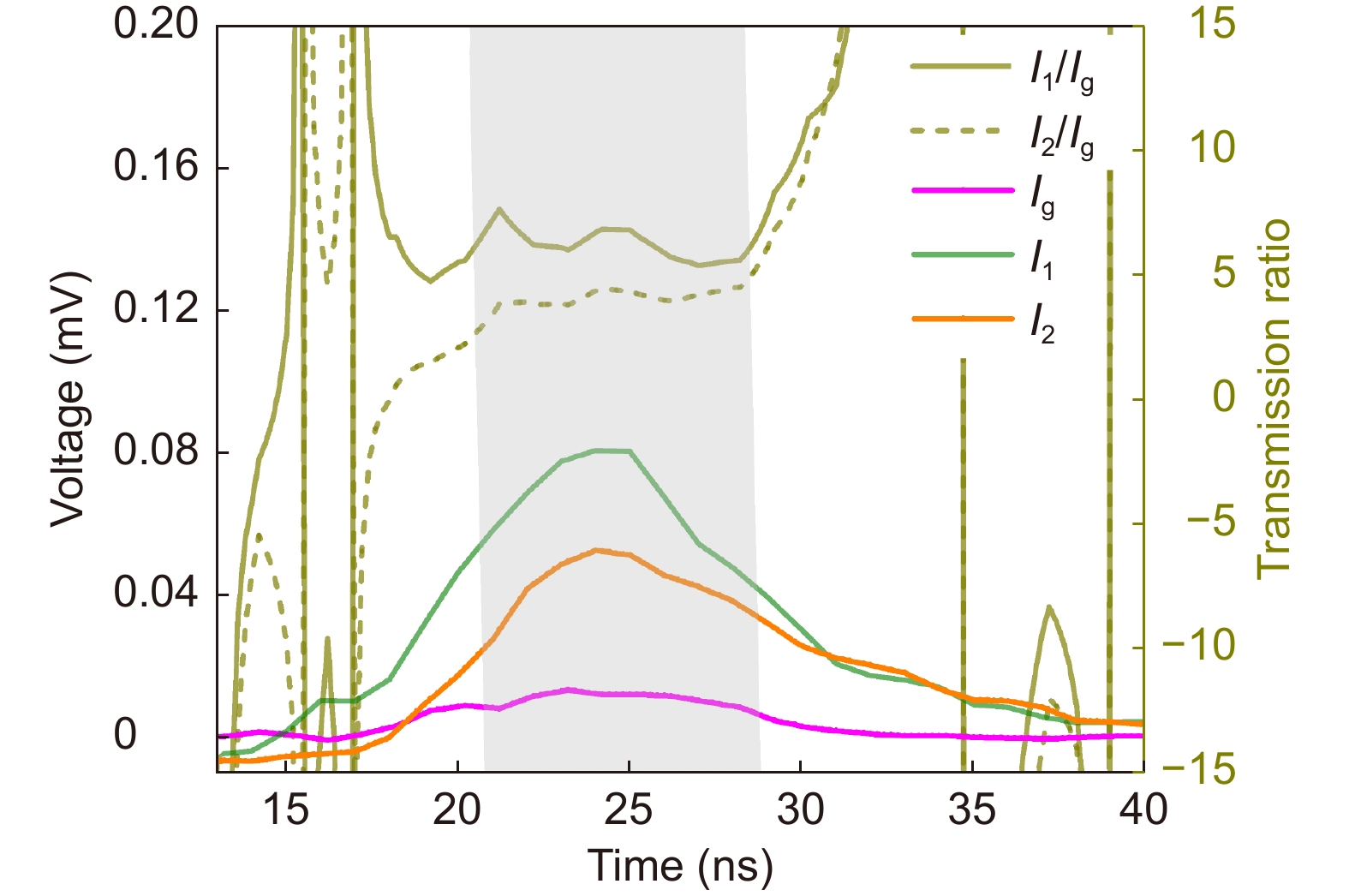
Figure 3. Spatially resolved Brillouin backscatter intensity from the water tank at room temperature recorded (a) by PMT1 (c) by PMT2 (e) by PMT3 with 200 successive shots (color lines) and their average (white dots) and the corresponding background noise measured by (b) by PMT1 (d) by PMT2 (f) by PMT3.In this experiment, there was some stray light, mainly caused by the laser light reflected from the lenses of the receiving telescope. The stray light can pass through the absorption filter and cannot be eliminated. As the distance between the telescope and the water tank is just 0.26 m, this stray light is mixed with the RB scattering signal and simultaneously detected by the PMTs. The background stray light was measured as illustrated in Fig. 3(b), 3(d), and 3(f), and subtracted from the data recorded by the three PMTs to extract the pure single. Fig. 4 shows the time dependence of the pure signal from PMT1 Ig, the pure signal from PMT2 I1, and the pure signal from PMT3 I2. The position of the peaks is where the light passes through the center of the water tank. By using the time-dependent voltages Ig, I1, and I2, the desired transmission ratios S1 = I1/Ig and S2 = I2/Ig of the double-edge filter are also displayed in Fig. 4 with a dark yellow color. Experimentally, in the ideal case, the transmission ratios should remain the same during the propagation of laser light in the water tank for each condition. However, due to the fluctuations of background noise and shot noise, the two ratios S1 and S2 are not flat signals. As illustrated in Fig. 4, the signals obtained during all instances of measurement show strong fluctuations, especially at the beginning and end of the measurement time, where the received signals are relatively weak; therefore, these signals cannot be entirely used. To obtain relatively stable ratios for each temperature and salinity for calibrations, a time window of 7 ns around the position of the peaks is chosen to determine the ratios S1 and S2, as shown in Fig. 4 with the gray region; the amplitude fluctuation is under 15% in this regime. The final ratios were obtained by averaging over this particular time window.
In this double-edge method, the transmission ratios are related to the Brillouin shift and linewidth. The relationships between the theoretical transmission ratios
S′1 andS′2 with the Brillouin shift and the Brillouin linewidth are easy to build based on simulation, following procedures as discussed in ref.25. As there is a difference between the theoretical ratios and the experimental voltage ratios S1 and S2, a calibration is required by mapping the experimental ratios to theoretical ratios; to achieve this, S1 and S2 were first recorded when water was set at different temperatures. Then, the calibration relationshipsSC1=F1(S1) between S1 andS′1 andSC2=F2(S2) based on S2 andS′2 are established. With these two relationships, based on the measured experimental voltage ratios S1 and S2, the calibration values ofSC1 andSC2 were obtained, as shown in Fig. 5(a). In addition, the calibration accuracy was tested by comparing the theoretical values of the Brillouin shift and linewidth to the values deduced from the calibration transmission ratios S1 and S2 at different temperatures, as shown in Fig. 5(b) and 5(c). The maximum difference between the theoretical and deduced values for Brillouin shift and linewidth are 4.3 MHz and 3.2 MHz, respectively. Figure 5. (a) Theoretical transmission ratios and the calibration of the transmission ratios in different temperatures. (b) Theoretical Brillouin shift and the shift deduced from calibration transmission ratios S1 and S2. (c) The theorical Brillouin linewidth and the linewidth deduced from calibration transmission ratios S1 and S2.
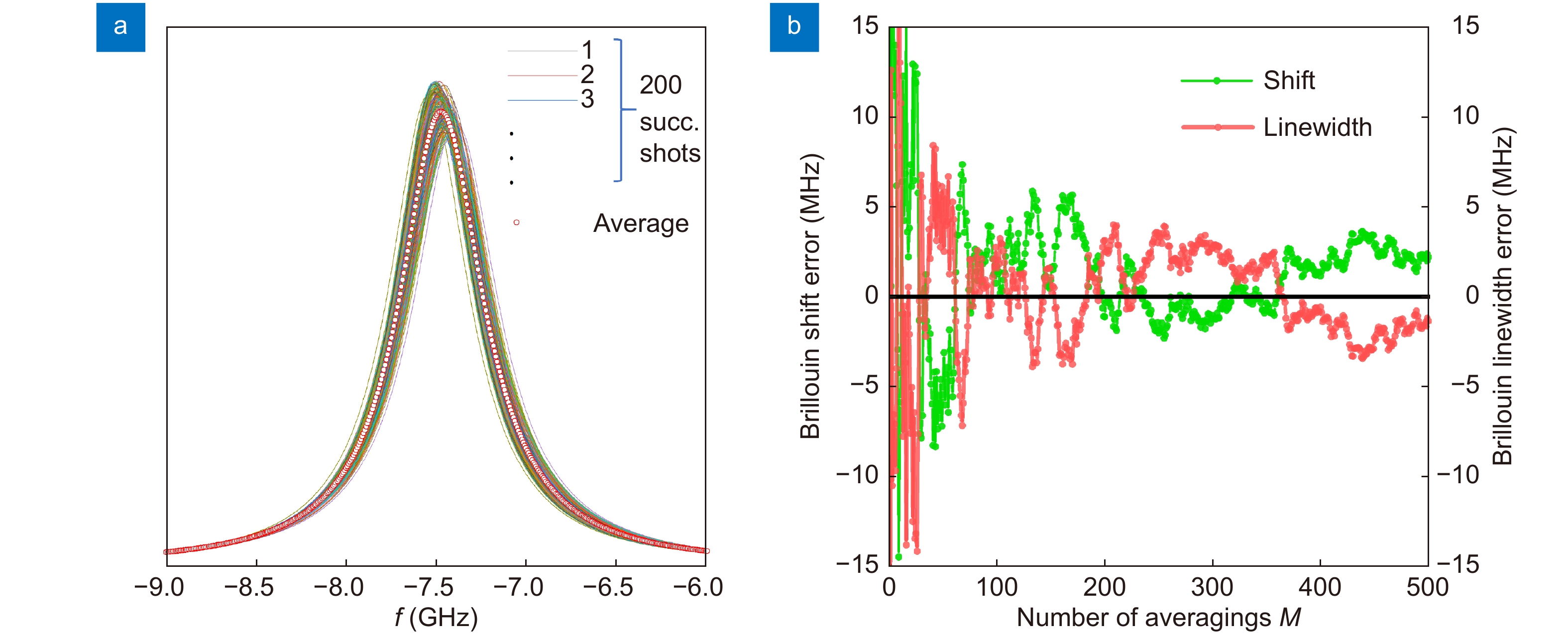
Figure 5. (a) Theoretical transmission ratios and the calibration of the transmission ratios in different temperatures. (b) Theoretical Brillouin shift and the shift deduced from calibration transmission ratios S1 and S2. (c) The theorical Brillouin linewidth and the linewidth deduced from calibration transmission ratios S1 and S2.After calibration, this setup can measure the Brillouin shift and linewidth of water to reconstruct the Brillouin spectrum and acquire information about temperature and salinity. To demonstrate the accuracy of the Brillouin spectrum with this method, the data for the water temperature of 20.4 °C were measured and the Brillouin spectrum was reconstructed as displayed in Fig. 6(a). Under this condition, the relative voltage ratios
SC1 andSC2 were 0.0274 and 0.0342, respectively, after calibration with averaging number of 170. Based on these ratios, the calculated Brillouin shiftvCB and Brillouin linewidthΓCB were determined to be 7.4515 GHz and 0.5734 GHz, respectively. For water at a temperature of 20.4 °C and salinity of 0%, the theoretical Brillouin shiftvTB and linewidthΓTB were 7.4459 GHz and 0.5772 GHz, respectively. The difference between thevCB andvTB as well as theΓCB andΓTB were 5.7 MHz and 3.8 MHz, respectively. Moreover, the corresponding simultaneously retrieved temperatures and salinity were 20.59 °C and 0.45%, respectively, and the differences between the experimental and theoretical predictions were 0.19 °C for temperature and 0.45% for salinity. With an increase in the averaging times, the accuracy of the Brillouin shift and Brillouin linewidth increased considerably. Figure 6(b) presents the changes in the errors of the Brillouin shift and Brillouin linewidth between the retrieved and theoretical values for the water temperature of 20.4 °C. It shows that when the averaging number is more than 500, the mean deviation for Brillouin shift and linewidth is less than 2.2 MHz and 1.4 MHz.This proposed method can realize the measurement of the Brillouin scattering spectrum and is used for simultaneous acquisition of temperature and salinity, which is important for water environment monitoring. To test its ability, five groups of experiments, named A, B, C, D and E, for water were performed. The water temperatures of the five groups were 20.4 °C, 22.6 °C, 24.8 °C, 26.6 °C and 28.2 °C, respectively; all water salinities were 0%. The measurement results are shown in Fig. 7.
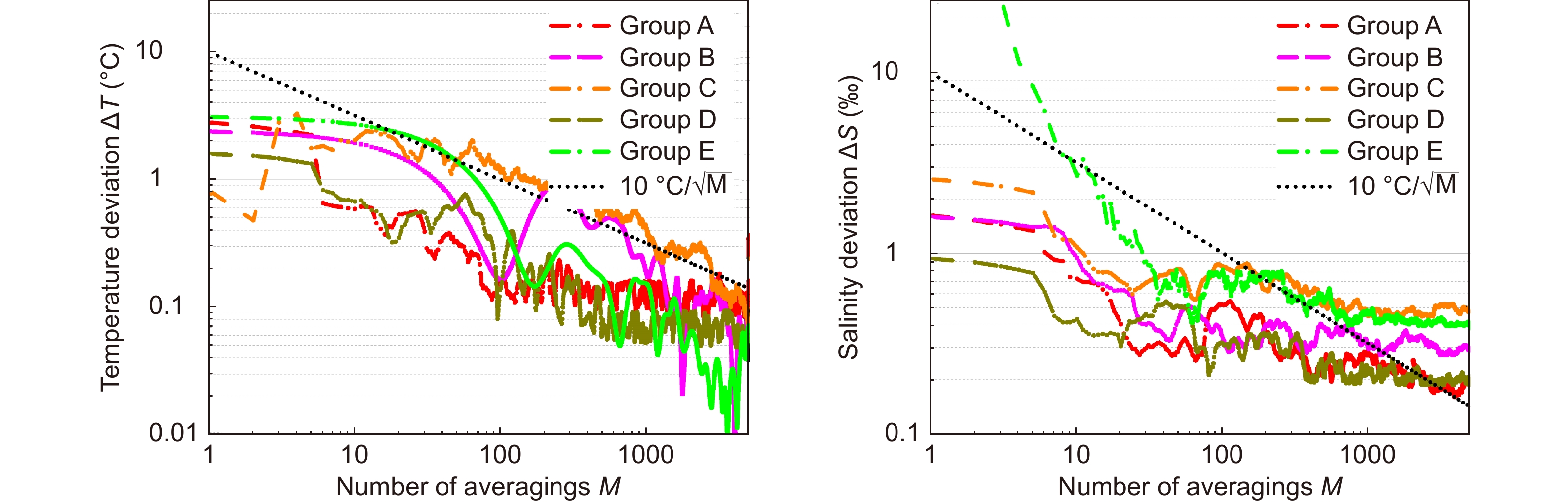 Figure 7. Absolute deviation of temperature and salinity between retrieved values and real values at different average numbers for the water in five groups of experiment. Water temperatures of the five groups are 20.4 °C, 22.6 °C, 24.8 °C, 26.6 °C and 28.2 °C, respectively; all the water salinities are 0%. Color lines represent the deviation and the black dots as reference line is the square root of the average number.
Figure 7. Absolute deviation of temperature and salinity between retrieved values and real values at different average numbers for the water in five groups of experiment. Water temperatures of the five groups are 20.4 °C, 22.6 °C, 24.8 °C, 26.6 °C and 28.2 °C, respectively; all the water salinities are 0%. Color lines represent the deviation and the black dots as reference line is the square root of the average number.Figure 7 depicts the absolute deviations of the temperature and salinity between the retrieved and real values at different averaging times. Color lines represent the deviation for different groups, and black dots represent the square root of the averaging number where a factor is multiplied for comparison purposes. Due to the randomness of the noise signal, the differences between the measured values and real values measured by the thermometer are large at a low number of averages. As the averaging number increased, the accuracy of the measured temperature and salinity was considerably enhanced. When the average number reaches 5000, the difference between the retrieved and actual temperature is less than 0.1 °C; for salinity, the difference is less than 0.5%. In general, the temperature deviations and salinity are inversely proportional to the square root of the averaging number. Nevertheless, the accuracy is limited by the shot noise due to the limited number of detected Brillouin-scattered photons. Due to the intrinsic error of the system, the measurement accuracy gradually tends to the limit with a further increase in the average number of times.
In the final system, used in real applications, the distance between the telescope and the surface of the liquid can be tuned to be longer. Correspondingly, the error induced by the background stray light was partly removed. The circuit design, optical elements, and path also need to be further optimized to improve the accuracy of the retrieved temperature and salinity. This improved method can realize the water profile measurement with high accuracy, showing a potential application prospect in marine surveys.
Conclusion
In summary, a method of Brillouin scattering spectrum measurement is proposed based on the double-edge technique. By detecting two edge energies of the Brillouin peak by a double-edge filter, the corresponding Brillouin shift and Brillouin linewidth can be calculated, and the Brillouin spectrum can be reconstructed. An experimental setup was built and carried out in water under different conditions to verify the effectiveness of this method. In this experiment, three signals—the reference Brillouin scattering energy and two edge energies of the Brillouin peak after a double-edge filter—were first recorded. After calibration, the Brillouin shift and linewidth were obtained and used for Brillouin spectrum reconstruction. The calibrated Brillouin shift and linewidth were compared with theoretical predictions to demonstrate the accuracy of the reconstructed spectrum. The differences between the calculated and theoretical values for Brillouin shift and linewidth were less than 4.3 MHz and 3.2 MHz, respectively. Furthermore, the experimental results indicate high accuracy of the retrieved temperature and salinity, up to 0.1 °C and 0.5%, respectively. This improved double-edge method has significant potential for applications in water profile measurements and oceanography.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 62175072, No. 62175072 and No. 12074209) and the Open Project of State Key Laboratory of Low-Dimensional Quantum Physics (Grant No. KF202008). Y. Wang acknowledges support from International Postdoctoral Exchange Fellowship Program (Talent-Introduction Program).
Author contributions
All authors commented on the manuscript.
Competing interests
The authors declare no competing financial interests.
-
References
[1] Strutt JW. On the light from the sky, its polarization and colour. Lond Edinb Dublin Philos Mag J Sci 41, 274–279 (1871). doi: 10.1080/14786447108640479 [2] Einstein A. Theorie der opaleszenz von homogenen flüssigkeiten und flüssigkeitsgemischen in der nähe des kritischen zustandes. Ann Phys 338, 1275–1298 (1910). doi: 10.1002/andp.19103381612 [3] Fabelinskii IL. Molecular Scattering of Light (Springer, New York, 1968). [4] Li ZT, Cao K, Li JS, Tang Y, Ding XR et al. Review of blue perovskite light emitting diodes with optimization strategies for perovskite film and device structure. Opto-Electron Adv 4, 200019 (2021). doi: 10.29026/oea.2021.200019 [5] Mandelstam LI. Light scattering by inhomogeneous media. Zh Russ Fiz Khim Ova 58, 381 (1926). [6] Brillouin L. Diffusion de la lumière et des rayons X par un corps transparent homogène. Ann Phys 9, 88–122 (1922). doi: 10.1051/anphys/192209170088 [7] Boley CD, Desai RC, Tenti G. Kinetic models and Brillouin scattering in a molecular gas. Can J Phys 50, 2158–2173 (1972). doi: 10.1139/p72-286 [8] Ma Y, Li H, Gu ZY, Ubachs W, Yu Y et al. Analysis of Rayleigh-Brillouin spectral profiles and Brillouin shifts in nitrogen gas and air. Opt Express 22, 2092–2104 (2014). doi: 10.1364/OE.22.002092 [9] Gu Z, Ubachs W, Marques Jr W, van de Water W. Rayleigh-Brillouin scattering in binary-gas mixtures. Phys Rev Lett 114, 243902 (2015). doi: 10.1103/PhysRevLett.114.243902 [10] Wang YQ, Ubachs W, de Moraes CAM, Marques Jr W. Rayleigh-Brillouin scattering in binary mixtures of disparate-mass constituents: SF6−He, SF6−D2, and SF6−H2. Phys Rev E 103, 013102 (2021). [11] Xu JQ, Witschas B, Kabelka PG, Liang K. High-spectral-resolution lidar for measuring tropospheric temperature profiles by means of Rayleigh–Brillouin scattering. Opt Lett 46, 3320–3323 (2021). doi: 10.1364/OL.424526 [12] Ma QH, Yang CX, Bruno D, Zhang J. Molecular simulation of Rayleigh-Brillouin scattering in binary gas mixtures and extraction of the rotational relaxation numbers. Phys Rev E 104, 035109 (2021). doi: 10.1103/PhysRevE.104.035109 [13] Mountain R D. Thermal relaxation and Brillouin scattering in liquids. J Res Natl Bur Stand A Phys Chem 70A, 207–220 (1966). doi: 10.6028/jres.070A.017 [14] Montrose CJ, Solovyev VA, Litovitz TA. Brillouin scattering and relaxation in liquids. J Acoust Soc Am 43, 117–130 (1968). doi: 10.1121/1.1910741 [15] Yoshida H, Hatae T, Fujita H, Nakatsuka M, Kitamura S. A high-energy 160-ps pulse generation by stimulated Brillouin scattering from heavy fluorocarbon liquid at 1064 nm wavelength. Opt Express 17, 13654–13662 (2009). doi: 10.1364/oe.17.013654 [16] Chaban I, Shin HD, Klieber C, Busselez R, Gusev V et al. Time-domain Brillouin scattering as a local temperature probe in liquids. MRS Adv 4, 9–14 (2019). doi: 10.1557/adv.2018.650 [17] Liu ML, Wu HB, Liu XM, Wang YR, Lei M et al. Optical properties and applications of SnS2 SAs with different thickness. Opto-Electron Adv 4, 200029 (2021). doi: 10.29026/oea.2021.200029 [18] Nelson DF, Lazay PD, Lax M. Brillouin scattering in anisotropic media: calcite. Phys Rev B 6, 3109–3120 (1972). doi: 10.1103/PhysRevB.6.3109 [19] Grimsditch MH, Ramdas AK. Brillouin scattering in diamond. Phys Rev B 11, 3139–3148 (1975). doi: 10.1103/PhysRevB.11.3139 [20] Crowhurst JC, Hearne GR, Comins JD, Every AG, Stoddart PR. Surface Brillouin scattering at high pressure: application to a thin supported gold film. Phys Rev B 60, R14990–R14993 (1999). doi: 10.1103/PhysRevB.60.R14990 [21] Comez L, Masciovecchio C, Monaco G, Fioretto D. Progress in liquid and glass physics by Brillouin scattering spectroscopy. Solid State Phys 63, 1–77 (2012). doi: 10.1016/B978-0-12-397028-2.00001-1 [22] Liu J, Shi MQ, Chen Z, Wang SM, Wang ZL et al. Quantum photonics based on metasurfaces. Opto-Electron Adv 4, 200092 (2021). doi: 10.29026/oea.2021.200092 [23] Mountain RD. Spectral distribution of scattered light in a simple fluid. Rev Mod Phys 38, 205–214 (1966). doi: 10.1103/RevModPhys.38.205 [24] Gong W, Dai R, Sun Z, Ren X, Shi J et al. Detecting submerged objects by Brillouin scattering. Appl Phys B 79, 635–639 (2004). doi: 10.1007/s00340-004-1590-7 [25] Schorstein K, Popescu A, Göbel M, Walther T. Remote water temperature measurements based on Brillouin scattering with a frequency doubled pulsed Yb: doped fiber amplifier. Sensors 8, 5820–5831 (2008). doi: 10.3390/s8095820 [26] Liang K, Ma Y, Yu Y, Huang J, Li H. Research on simultaneous measurement of ocean temperature and salinity using Brillouin shift and linewidth. Opt Eng 51, 066002 (2012). doi: 10.1117/1.OE.51.6.066002 [27] Rudolf A, Walther T. Laboratory demonstration of a Brillouin lidar to remotely measure temperature profiles of the ocean. Opt Eng 53, 051407 (2014). doi: 10.1117/1.OE.53.5.051407 [28] Fry ES, Emery Y, Quan XH, Katz JW. Accuracy limitations on Brillouin lidar measurements of temperature and sound speed in the ocean. Appl Opt 36, 6887–6894 (1997). doi: 10.1364/AO.36.006887 [29] Liu DH, Xu JF, Li RS, Dai R, Gong WP. Measurements of sound speed in the water by Brillouin scattering using pulsed Nd: YAG laser. Opt Commun 203, 335–340 (2002). doi: 10.1016/S0030-4018(02)01181-1 [30] Xu JF, Ren XB, Gong WP, Dai R, Liu DH. Measurement of the bulk viscosity of liquid by Brillouin scattering. Appl Opt 42, 6704–6709 (2003). doi: 10.1364/AO.42.006704 [31] Ge Y, Shi JL, Zhu KX, He XD. Determination of bulk viscosity of liquid water via pulse duration measurements in stimulated Brillouin scattering. Chin Opt Lett 11, 112902 (2013). doi: 10.3788/COL201311.112902 [32] Liu J, Shi JL, He XD, Li SJ, Chen XG et al. Comparison of three technique of Brillouin lidar for remote sensing of the ocean. Opt Commun 352, 161–165 (2015). doi: 10.1016/j.optcom.2015.04.086 [33] Shi J, Ouyang M, Gong W, Li S, Liu D. A Brillouin lidar system using F–P etalon and ICCD for remote sensing of the ocean. Appl Phys B 90, 569–571 (2008). doi: 10.1007/s00340-007-2866-5 [34] Huang J, Ma Y, Zhou B, Li H, Yu Y et al. Processing method of spectral measurement using F-P etalon and ICCD. Opt Express 20, 18568–18578 (2012). doi: 10.1364/OE.20.018568 [35] Bl/achowicz T, Bukowski R, Kleszczewski Z. Fabry–Perot interferometer in Brillouin scattering experiments. Rev Sci Instrum 67, 4057–4060 (1996). doi: 10.1063/1.1147550 [36] Emery Y, Fry ES. Laboratory development of a LIDAR for measurement of sound velocity in the ocean using Brillouin scattering. Proc SPIE 2963, 210–215 (1997). doi: 10.1117/12.266444 [37] Rupp D, Zipf A, Kress M, Lux K, Walther T et al. A Brillouin lidar for remote sensing of the temperature profile in the ocean — towards a simultaneous measurement of temperature and salinity. In OCEANS 2017 - Anchorage 1–7 (IEEE, 2017); https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8232330. [38] Liang K, Zhang R, Sun Q, Xu Y, Wu H et al. Brillouin shift and linewidth measurement based on double-edge detection technology in seawater. Appl Phys B 126, 160 (2020). doi: 10.1007/s00340-020-07509-1 Cited by(42)
-
Access History
-
Figure 1.
(a) Vector diagram of Brillouin scattering in view of quantum physics with the process of incident photon releasing and absorbing a phonon. (b) Brillouin spectra of water varies as the temperature changes. (c) Principle of the Brillouin spectrum measurement using double edge technique. Two edge filters are set at the steep edge of the Brillouin Stokes spectrum BS(vB, ΓB ), where vB is the Brillouin shift ΓB and is the Brillouin linewidth. For BS, the energies after these two filters are I1(vB, ΓB ) and I2(vB, ΓB). vB and ΓB can be deduced from I1 and I2, and Brillouin spectrum BS can be reconstructed. When the Brillouin spectrum changes to BS′, new energies
I′1 I′2 -
Figure 2.
Sketch of experimental apparatus. Pulse light of wavelength 532.293 nm with pulse width of approximately 7.5 ns, repetition rate of 100 Hz, and pulse energy of 20 mJ goes through a half waveplate, a polarization beam splitter (PBS), and a quarter-wave plate successively. Then the light is spread by a telescope combined by two convex lenses, L1 (f=0.5 m) and L2 (f = 0.1 m), and yields into a water tank of 1.8 m length and 0.5 m width to produce scattering light. The 180º back scattering light is received by the telescope and reflected by the PBS to an iodine tube which can absorb the Rayleigh part. The scattering light after the iodine tube is split into two by M2. One small fraction beam is detected by the first photomultiplier tube (PMT1) as reference energy. The other part enters to a double-edge filter which is made by two Fabry-Perot interferometers and the light beams after these two interferometers are accepted by PMT2 and PMT3 separately. D is diaphragm, Mi and Li (i=1, 2..) are mirrors and lens, respectively.
-
Figure 3.
Spatially resolved Brillouin backscatter intensity from the water tank at room temperature recorded (a) by PMT1 (c) by PMT2 (e) by PMT3 with 200 successive shots (color lines) and their average (white dots) and the corresponding background noise measured by (b) by PMT1 (d) by PMT2 (f) by PMT3.
-
Figure 4.
Signals after subtracting background noise from the data obtained from three PMTs, Ig, I1 and I2, and the two transmission ratios are plotted (dark yellow). The gray region where the received signals are strong relatively shows the ratios that do not vary a lot.
-
Figure 5.
(a) Theoretical transmission ratios and the calibration of the transmission ratios in different temperatures. (b) Theoretical Brillouin shift and the shift deduced from calibration transmission ratios S1 and S2. (c) The theorical Brillouin linewidth and the linewidth deduced from calibration transmission ratios S1 and S2.
-
Figure 6.
(a) Reconstructed Brillouin spectrum with 200 successive shots (color lines) and their average (white dots). (b) Errors of Brillouin shift and linewidth between the retrieved value and theorical value when the recorded signal averaged from 1 to 500 times for water in 20.4 °C.
-
Figure 7.
Absolute deviation of temperature and salinity between retrieved values and real values at different average numbers for the water in five groups of experiment. Water temperatures of the five groups are 20.4 °C, 22.6 °C, 24.8 °C, 26.6 °C and 28.2 °C, respectively; all the water salinities are 0%. Color lines represent the deviation and the black dots as reference line is the square root of the average number.


 E-mail Alert
E-mail Alert RSS
RSS



 DownLoad:
DownLoad: